이진 탐색 트리란?(What is a Binary search tree?)
이진 탐색 트리(Binary Search Tree, BST)는 이진 트리에서 자료의 탐색, 삽입, 삭제를 효율적으로 하기 위해 만들어진 트리이다. 연결 리스트의 경우 삽입, 삭제시 O(1)의 시간 복잡도를 가진다. 그러나 자료를 탐색하는 경우 O(n)의 시간 복잡도를 가진다. 반면 이진 탐색 트리의 경우 트리의 높이를 h라고 했을 때 O(h)의 시간 복잡도를 가진다.(노드의 개수를 n이라고 하면 O(Log n)의 시간 복잡도를 가짐) 다음은 이진 탐색 트리의 정의이다.
정의
이진 탐색 트리는 공백이 가능한 이진 트리로서, 공백이 아닐 경우 다음의 조건들을 만족한다.
- 모든 노드는 이진 탐색 트리내에서 유일한 키를 갖는다.
- 임의의 노드 n에 대해, 왼쪽 서브 트리가 공백이 아니라면 이 서브 트리에 존재하는 모든 노드들의 키 값은 노드 n의 키 값보다 작아야 한다.
- 임의의 노드 n에 대해, 오른쪽 서브 트리가 공백이 아니라면 이 서브 트리에 존재하는 모든 노드들의 키 값은 노드 n의 키 값보다 커야 한다.
- 임의의 노드 n에 대한 왼쪽 서브 트리와 오른쪽 서브 트리 또한 이진 탐색 트리이다.

일반 이진 트리의 경우, 값이 들어오는 순서대로 트리에 넣는다. 하지만 이진 탐색 트리는 값의 크기에 따라 삽입되는 노드의 위치가 달라진다. 위 그림에서는 D를 기준으로 사전적인 순서가 앞에 있는 B는 부모노드의 오른쪽에 들어가고 순서가 뒤에 있는 E는 부모노드의 오른쪽에 들어가게 된다.
이진 탐색 트리의 탐색(BST search operation)
이진 탐색 트리에서의 탐색 연산은 루트 노드를 기점으로 찾고자 하는 값의 크기에 따라 왼쪽 서브 트리나 오른쪽 서브 트리로 이동하여 노드를 탐색한다. 현재 노드의 값보다 찾는 값이 크면 오른쪽 서브 트리에서 탐색을 진행하고 값이 작다면 왼쪽 서브 트리에서 검색을 진행한다. 검색은 재귀적인 방법과 반복적인 방법으로 구현이 가능하다. 이진 탐색 트리에서 값 C를 탐색하는 과정은 다음과 같다.
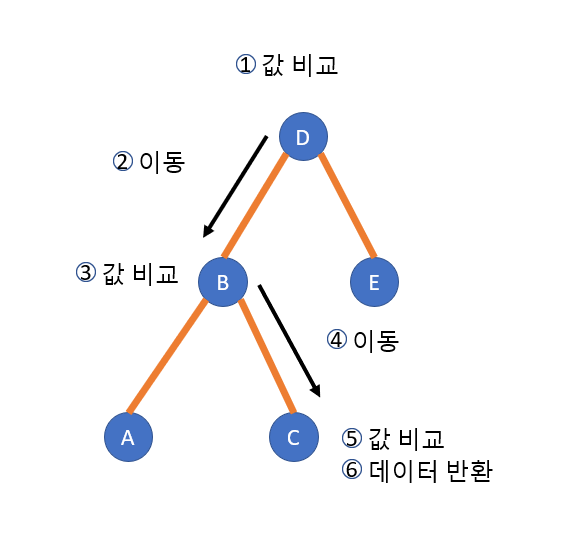
만약 값이 트리에 없다는 건 어떻게 알까? 위에서 F값을 찾는다면 E까지 검색한 후 F는 사전적 순서가 뒤에 E보다 뒤에 있기 때문에 오른쪽 서브트리로 이동을 할 것이다. 하지만 E의 오른쪽 서브 트리는 NULL의 상태를 가짐으로 E의 오른쪽 서브 트리는 존재하지 않는다는 것을 알 수 있다. 그렇기 때문에 검색 도중 NULL을 만나면 검색을 실패했다는 것을 알 수 있다.
이진 탐색 트리의 삽입(BST Insert operation)
이진 탐색 트리에서의 삽입 연산도 어렵지 않다. 탐색 과정에서 NULL을 만나면 삽입을 진행하는 방식으로 구현할 수 있다. 이때 이진 탐색 트리의 특성인 중복된 키 값이 존재하지 않는다는 특성을 유지하기 위해 탐색에 성공하면 삽입을 하지 않는다. 삽입 과정은 다음과 같다.

이진 탐색 트리의 삭제(BST Delete operation)
이진 탐색 트리의 삭제는 삽입과 반대로 하면 된다. 우리가 삽입을 할 때 키 값이 존재하면 삽입 연산을 하지 않았는데 삭제 과정에서는 반대로 키 값이 존재하면 삭제 연산을 수행한다. 다만 주의해야 할 점이 있다면 삭제를 할 때는 삭제하려는 노드의 자식 노드의 개수에 따라 삭제 방법이 달라진다.
1. 자식 노드가 없는 경우
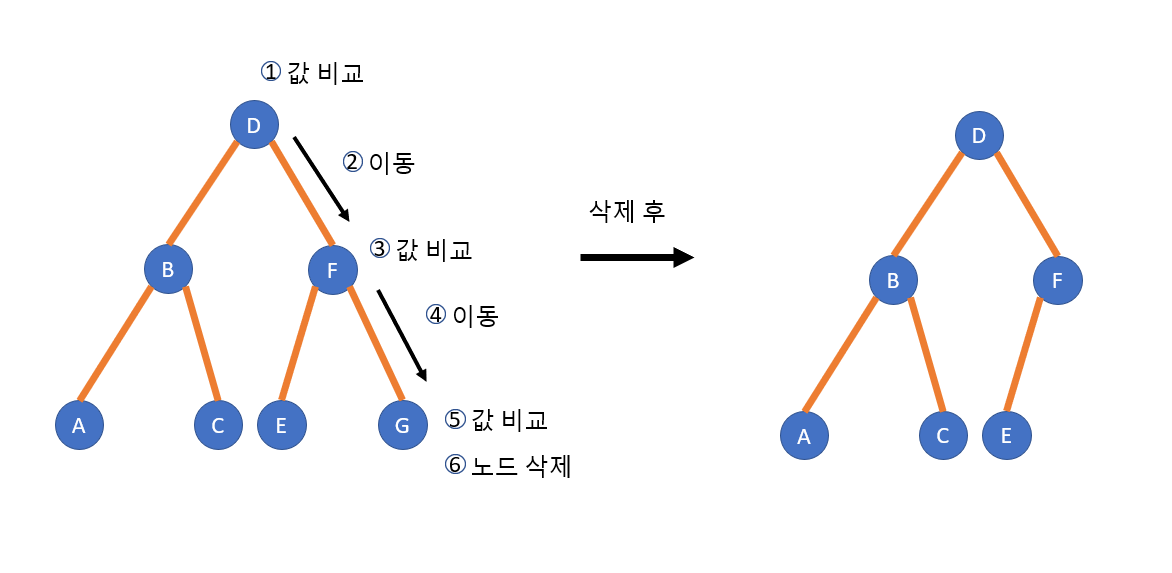
자식 노드가 없는 경우는 삭제할 키 값을 탐색하고 삭제할 키 값이 존재하면 삭제 연산을 진행하고 키 값이 존재하지 않으면 삭제 연산에 실패했음을 알린다.
2. 자식 노드가 1개인 경우
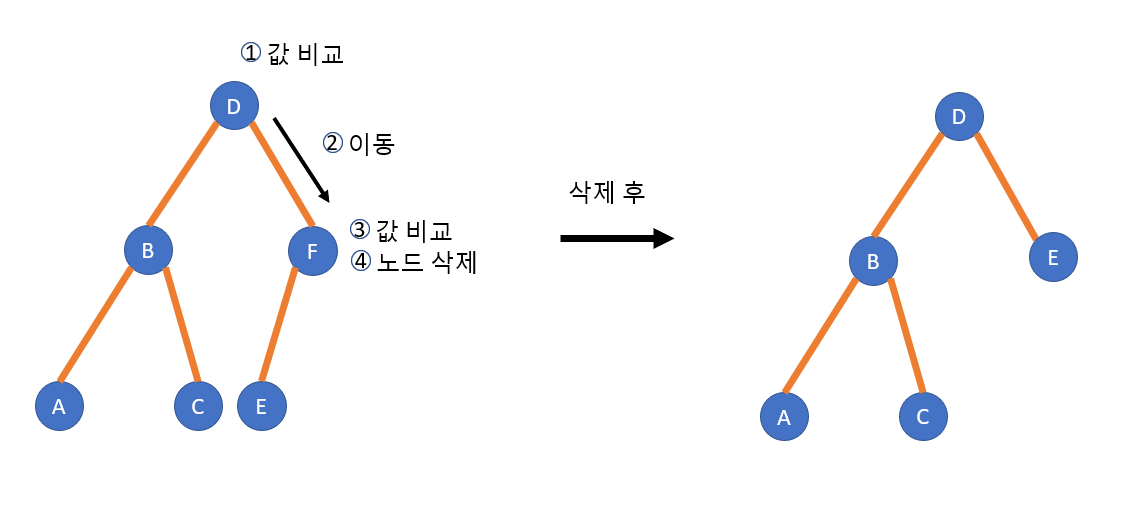
자식 노드가 1개인 경우 삭제하는 노드의 서브 트리를 삭제할 노드의 위치로 가져온다.
3. 자식 노드가 2개인 경우

자식 노드가 2개가 있는 경우는 조금 까다롭다. 먼저 삭제할 노드를 탐색한 후, 삭제할 노드가 존재하면 삭제할 노드를 대체할 노드를 선택한 후 바꿔준다. 대체 노드를 선택하는 방법에는 2가지가 있는데 하나는 삭제할 노드의 왼쪽 서브 트리에서 가장 큰 노드로 대체하는 방법이고 다른 하나는 삭제할 노드의 오른쪽 서브 트리에서 가장 작은 노드로 대체하는 방법이 있다. 위 그림에서는 전자의 방법을 택했다. 삭제할 노드를 대체하면 삭제할 노드의 자식 노드 유무를 검사하고 자식 노드가 있다면 적절히 위치를 변경한다. 위에 그림에서는 없지만 C 노드의 왼쪽에 노드가 존재하면 B 노드의 오른쪽으로 노드의 위치를 변경한다. 그 후 삭제할 노드를 삭제하면 된다.
완전 이진 탐색 트리(Complete Binary Search Tree)
이진 탐색 트리는 자료를 탐색하는데 최적화된 트리이다. 하지만 자료가 오름차순이나 내림차순과 같은 순서대로 입력되면 트리가 한쪽으로만 만들어지는 형태가 된다. 이는 연결 리스트와 다를 바 없는 형태로 이진 탐색 트리의 장점인 빠른 검색 속도를 이용하지 못한다. 이를 해결하기 위해 나온 것이 완전 이진 탐색 트리이다.

완전 이진 탐색 트리(Complete binary search tree)는 완전 이진 트리의 성질을 가지는 이진 탐색 트리이다. 완전 이진 탐색 트리는 편향된 이진 탐색 트리와는 다르게 항상 O(log n)의 검색 속도를 보장한다. 그러나 완전 이진 탐색 트리의 단점은 트리에 자료가 삽입될 때마다 완전 이진 탐색 트리의 형태를 유지하기 위해 트리의 모양을 바꾸어야 한다. 즉, 삽입할 때 많은 시간이 소요된다는 것이다. 삽입이 적고 탐색이 많은 경우에는 유리할 수 있으나 삽입하는 빈도수가 높아지면 높아질수록 효율성이 떨어진다. 이런 불편함을 해결한 것이 AVL트리이다.
이진 탐색 트리의 구현
구현은 아래 필자의 깃허브에 있으니 참고하길 바란다. 기본적인 원리만 구현을 했기 때문에 실제 사용에는 무리가 있다.참고만 하길 바란다. 트리 구현에 대한 자세한 설명은 추후에 포스팅하겠다.
GitHub - LimeTree0/Data-Structure
Contribute to LimeTree0/Data-Structure development by creating an account on GitHub.
'자료구조' 카테고리의 다른 글
| 그래프(Graph) (0) | 2022.03.30 |
|---|---|
| AVL 트리(AVL Tree) (0) | 2022.03.29 |
| 일반 트리에서 이진 트리로 변환 (0) | 2022.03.29 |
| 스레드 이진 트리(Threaded binary tree) (0) | 2022.03.03 |
| 트리 순회(Tree Traversal) (0) | 2022.03.01 |