LimeCoding

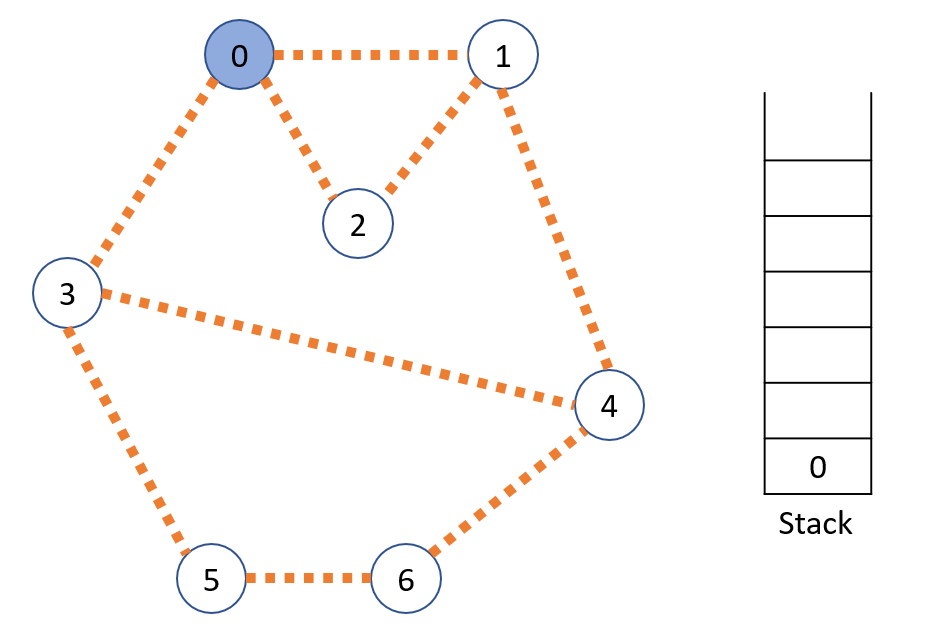
신장 트리란?(What is a Spanning Tree?) 앞서 포스팅에서 깊이 우선 탐색과 너비 우선 탐색에 대해 다루었다. 연결 그래프 G = (V, E)에 대해서 깊이 우선 탐색이나 너비 우선 탐색을 하게 되면 정점들을 방문하면서 지나는 엣지들을 보면 트리 형태의 모양을 띄게 된다. 이러한 그래프를 탐색하면서 지나게 되는 엣지들의 집합을 트리 엣지(tree edge)라고 하고 트리 엣지를 제외한 나머지 엣지들을 비트리 엣지(nontree edge)라고 한다. 깊이 우선 탐색이나 너비 우선 탐색을 하게 되면 생기는 트리엣지로 이루어진 사이클을 갖지 않는 최소 부분 그래프가 생기는데 이 부분 그래프를 그래프 G에 대한 신장 트리라고 한다. 만약 n개의 정점을 가지는 그래프가 있다면 n개의 정점을 모두..

너비 우선 탐색(Breadth First Search)는 BFS라고도 하며 그래프를 순회하는 방법중 하나이다. 너비 우선 탐색은 깊이 우선 탐색과 다르게 인접한 정점을 모두 방문한 후 정점을 방문한 순서대로 다시 모든 인접한 정점을 방문하는 방식의 탐색 방법이다. 너비 우선 탐색은 큐로 구현을 할 수 있다. 너비 우선 탐색 방법은 다음과 같다. 너비 우선 탐색이 시작될 정점 v를 선택한다. 선택된 정점 v에 대해 방문 표시와 방문 처리를 하고 큐에 삽입한다. 큐의 front에서 꺼낸 정점의 인접 정점들에 대해 방문되지 않은 정점들을 큐에 삽입하고 방문 처리를 한다. 큐가 공백이 될 때까지 3의 과정을 반복한다. 다음은 너비 우선 탐색의 예시이다. 정점 0 방문 정점 0을 방문한 후 큐에 0을 넣는다. 정..

깊이 우선 탐색(Depth First Search)은 DFS라고도 불리며 그래프를 순회하는 방법 중에 하나이다. 깊이 우선 탐색은 한 정점을 기준으로 인접한 정점을 방문한 뒤 방문한 정점을 기준으로 다시 인접한 정점을 방문하는 방식의 재귀적인 방법으로 방문을 한다. 깊이 우선 탐색은 다음과 같은 방법으로 진행된다. 깊이 우선 탐색을 시작할 정점을 선택한다. 선택된 정점을 방문 처리한다. 정점 v에 인접한 정점들에 대해 3-1. 방문되지 않은 정점이 존재하면 정점 v를 스택에 push하고, v의 인접 정점들 가운데 방문되지 않은 정점 w를 선택하여 2의 과정부터 다시 시작한다. 3-2. 방문되지 않은 정점이 존재하지 않는다면 가장 최근에 스택에 push된 정점을 pop하여 3의 과정부터 다시 사작한다. s..

인접 행렬(Adjacency Matrix) 컴퓨터로 그래프를 표현하는 방법중 하나는 인접 행렬이다. 인접 행렬은 배열을 이용하여 표현한다. 여기서 배열의 행은 출발 노드를 가리키고 열은 도착 노드를 가리킨다. 두 노드의 경로가 존재하면 1, 존재하지 않으면 0으로 표기한다. 무방향 그래프는 1->0과 0->1로 가는 경로를 모두 표기하고 방향 그래프는 해당 경로가 있는 경우에만 표시를 한다. 위 표를 자세히 보면 알 수 있는 재미있는 사실이 하나 있다. 그건 바로 첫 번째 그래프와 두 번째 그래프의 인접 행렬은 모두 대각선에 대해 대칭 형태를 보여준다. 그렇기 때문에 대각선으로 나누어지는 배열의 반만 있어도 그래프를 표현할 수 있다. 세 번째 그래프의 경우도 1보다는 0이 더 많은 것을 볼 수 있다. 이..

그래프란?(What is a Graph?) 그래프의 개념은 1736년 수학자 레온하르트 오일러가 쾨니히스베르크의 다리에 대한 문제를 풀면서 처음 등장했다. 오일러는 각 섬을 정점으로 표현하고 다리는 엣지로 표현하면서 모든 다리를 한번씩만 거쳐서 원래대로 돌아오는 방법은 존재하지 않는다는 것을 증명했다. 이러한 그래프는 현대에 와서는 전기 회로의 분석, 최단 경로 검색, 컴퓨터 통신 네트워크, 인공지능등 많은 분야에서 사용되고 있다. 자료구조에서 그래프(graph)는 공집합이 아닌 정점들(vertex)의 집합과 이 정점들을 서로 연결하는 엣지들의 집합으로 정의할 수 있다. 그래프에서 정점(vertex)은 데이터를 가지는 노드이며, 서로 다른 두 정점을 잇는 선을 엣지(edge) 또는 간선이라고 한다. 그래..

이전 포스팅에서 완전 이진 탐색 트리에 대해 설명했지만 이 포스팅을 통해 들어온 사람들을 위해 다시 설명한 후 AVL트리를 설명하겠다. 완전 이진 탐색 트리(Complete Binary Search Tree) 이진 탐색 트리는 자료를 탐색하는데 최적화된 트리이다. 하지만 자료가 오름차순이나 내림차순과 같은 순서대로 입력되면 트리가 한쪽으로만 만들어지는 형태가 된다. 이는 연결 리스트와 다를 바 없는 형태로 이진 탐색 트리의 장점인 빠른 검색 속도를 이용하지 못한다. 이를 해결하기 위해 나온 것이 완전 이진 탐색 트리이다. 완전 이진 탐색 트리(Complete binary search tree)는 완전 이진 트리의 성질을 가지는 이진 탐색 트리이다. 완전 이진 탐색 트리는 편향된 이진 탐색 트리와는 다르게..

이진 탐색 트리란?(What is a Binary search tree?) 이진 탐색 트리(Binary Search Tree, BST)는 이진 트리에서 자료의 탐색, 삽입, 삭제를 효율적으로 하기 위해 만들어진 트리이다. 연결 리스트의 경우 삽입, 삭제시 O(1)의 시간 복잡도를 가진다. 그러나 자료를 탐색하는 경우 O(n)의 시간 복잡도를 가진다. 반면 이진 탐색 트리의 경우 트리의 높이를 h라고 했을 때 O(h)의 시간 복잡도를 가진다.(노드의 개수를 n이라고 하면 O(Log n)의 시간 복잡도를 가짐) 다음은 이진 탐색 트리의 정의이다. 정의 이진 탐색 트리는 공백이 가능한 이진 트리로서, 공백이 아닐 경우 다음의 조건들을 만족한다. 모든 노드는 이진 탐색 트리내에서 유일한 키를 갖는다. 임의의 노..

일반 트리는 차수가 불규칙하기 때문에 자료를 처리할 때 이진 트리에 비해 비효율적인 면이 있다. 그렇기 때문에 일반 트리를 이진 트리로 변환해야 할 때가 있다. 일반 트리를 이진 트리로 변환하는 방법은 다음과 같다. 먼저 각 부모 노드당 2개의 노드만 가지도록 부모 노드의 왼쪽 자식과 오른쪽 형제를 연결한다. 다음 적절한 각도로 트리를 회전시킨다.(대부분 45도로 회전하라고 한다.) 회전한 트리를 적절하게 재배치를 하면 이진 트리가 된다.

스레드 이진 트리란?(What is treaded binary tree?) ​이진 트리를 연결 리스트로 표현했을 때 각 노드당 2개의 링크필드를 가지므로 n개의 노드에 대해 2n개의 링크필드를 가진다. 이때 마지막 노드가 n+1개의 링크필드를 가지는데 이 링크필드 모두 NULL을 가리켜 메모리 낭비가 심하다. 이를 해결하기 위해 펄리스(Perlis)와 손톤(Thornton)이 NULL링크들이 특정 노드를 가리키도록 하는 방법을 만든다. 여기서 조정된 NULL링크를 스레드(thread)라고 한다. 스레드 이진 트리는 기존 이진 트리의 구조에 2개의 쓰레드를 추가한다. 스레드 이진 트리에서 왼쪽 스레드와 오른쪽 스레드는 순회 방법에 따라 각각 특정 노드의 오른쪽 링크와 왼쪽 링크가 직전 방문 노드와 다음 방..

트리 순회(Tree Traversal) 배열은 인덱스를 통해 모든 데이터를 접근할 수 있다. 연결 리스트의 경우도 처음부터 끝까지 링크를 통해 접근할 수 있다. 하지만 트리는 선형 자료구조가 아니기 때문에 트리를 선형 자료 구조와 같은 방법으로 접근할 수 없다. 그렇다면 트리 구조에서 모든 데이터를 보고 싶다면 어떻게 해야할까? 트리에서는 순회(traversal)를 통해 모든 노드들을 접근할 수 있다. 트리를 순회하는 방법은 노드를 방문하는 순서에 따라 전위(preorder), 중위(inorder), 후위(postorder), 레벨(level)로 나뉜다. 전위 순회(Preorder Traversal) 전위 순회(preorder traversal)는 루트 노드를 먼저 방문한 후 이 노드의 왼쪽 서브트리를 ..