이분 검색이란?(What is binary search?)
이전 포스팅에서 작성한 순차 검색은 최대 n이라는 시간이 걸리는 검색 방법이다. 그렇기에 n이 100만, 1000만이 되면 검색하는데 상당히 많은 시간이 소요된다. 이를 해결하기 위한 알고리즘이 바로 이분 검색이다. 이분 검색은 대표적인 분할 정복 알고리즘이다. 이러한 분할 정복 알고리즘은 반복문으로 고쳐주면 더 빠른 성능을 낼 수 있다. 이분 검색의 작동 방식은 다음과 같다.
- 배열의 중간 요소와 찾고자하는 값을 비교한다. 이때 찾고자하는 값이 배열의 중간 요소이면 값을 리턴하고 종료한다.
- 배열을 반으로 나눈다.
- 중간 요소를 기준으로 찾는 값이 작으면 왼쪽 배열을, 크면 오른쪽 배열을 탐색한다.
- 1~3을 반복한다.
이분 검색 알고리즘(Binary search Algorithm)
int location (int low, int high)
{
int mid;
if (low > high) return 0;
else {
mid = floor_function((low + high)/2);
if (x == S[mid]) return mid;
else if (x < S[mid]) return location(low, mid - 1);
else return location(mid + 1, high);
}
}위 의사코드는 이분 검색 알고리즘의 의사코드이다. mid는 배열의 중간을 가리키고 S는 입력 배열이다. x는 찾고자하는 값이며 low, high는 배열의 양 끝을 의미한다. floor_function은 바닥 함수로 임의의 실수보다 작거나 같은 정수를 의미한다.

이분 검색 최악의 경우(Worst case of B.S)

Lower bound와 Upper bound(Lower bound and Upper bound)
이분 탐색은 정렬된 배열에서 특정값을 빠르게 찾기 위해 사용하는 탐색 알고리즘이다. 그러나 배열에 특정값이 여러 개 존재한다면 어떤 방식으로 검색을 해야 할까? 이 알고리즘을 조금 변형하면 이런 문제를 해결할 수 있다. 그것이 바로 Lower bound와 Upper bound이다.

Lower bound
lower bound는 내가 찾고자 하는 값이 x일 때 x 이상이 되는 첫 번째 원소의 위치를 찾는 방법이다. 알고리즘은 다음과 같다.
- low를 배열의 가장 작은 인덱스로 설정하고 high를 가장 큰 인덱스로 설정한다.
- mid = ( low + high ) / 2를 한다.
- 만약 arr[mid] < target이면, low = mid + 1로 설정한다.
- 3번을 만족하지 않는다면 high = mid로 설정한다.
- low < high를 만족하는 동안 1부터 4 과정을 반복한다.
- 반복이 끝나면 low값을 리턴한다.
다음은 5를 lower bound로 찾는 과정을 그림으로 나타낸 것이다.
- low와 high를 각각 배열의 최소 인덱스와 최대 인덱스로 설정한다.
mid = (low + high) / 2 = 6으로 둔다.
5 <= arr[mid]이므로 high = mid = 6으로 설정한다.
- mid = (low + high) / 2 = 3으로 둔다.
arr[mid] < 5이므로 low = mid + 1 = 4로 설정한다.
- mid = (low + high) / 2 = 5로 둔다.
5 <= arr[mid]이므로 high = mid = 5로 설정한다.
- mid = (low + high) / 2 = 4로 둔다.
arr[mid] < 5이므로 low = mid + 1 = 5로 설정한다.
- low == high가 되면서 low < high 조건을 만족하지 않음으로 반복을 종료한다.

- 반복이 끝났으므로 low를 리턴한다.
lower bound 코드 구현
// lowerBound 함수 구현
public static int lowerBound(int[] arr, int target) {
int low = 0;
int high = arr.length;
while (low < high) {
int mid = (low + high) / 2;
if (arr[mid] < target) {
low = mid + 1;
} else {
high = mid;
}
}
return low; // lower bound 위치 반환
}Upper bound
upper bound는 내가 찾고자 하는 값이 x일 때 x를 처음으로 초과하는 인덱스를 찾는 방법이다. 알고리즘은 다음과 같다.
- low를 배열의 가장 작은 인덱스로 설정하고 high를 가장 큰 인덱스로 설정한다.
- mid = ( low + high ) / 2를 한다.
- 만약 target < arr[mid]이면, high = mid로 설정한다.
- 3번을 만족하지 않는다면 low = mid + 1로 설정한다.
- low < high를 만족하는 동안 1부터 4 과정을 반복한다.
- 반복이 끝나면 low값을 리턴한다.
다음은 5를 upper bound로 찾는 과정을 그림으로 나타낸 것이다.
- low와 high를 각각 배열의 최소 인덱스와 최대 인덱스로 설정한다.
mid = (low + high) / 2 = 6으로 둔다.
arr[mid] <= 5이므로 low = mid + 1 = 7로 설정한다.
- mid = (low + high) / 2 = 9로 둔다.
arr[mid] > 5이므로 high = mid = 9로 설정한다.
- mid = (low + high) / 2 = 8로 둔다.
arr[mid] > 5이므로 high = mid = 8로 설정한다.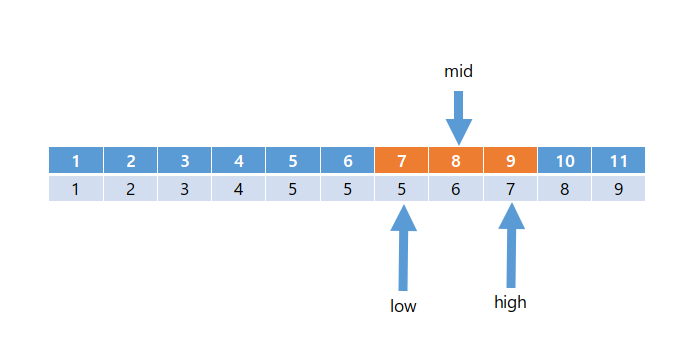
- mid = (low + high) / 2 = 7로 둔다.
5 <= arr[mid]이므로 low = mid + 1 = 8로 설정한다.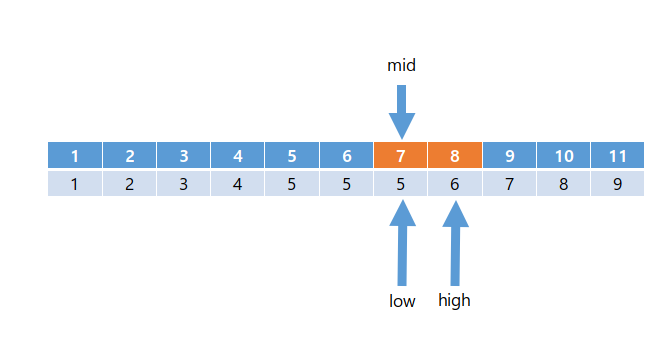
- low == high가 되면서 low < high 조건을 만족하지 않음으로 반복을 종료한다.
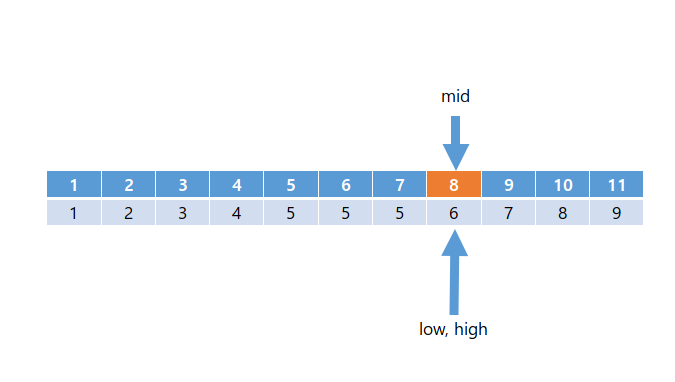
- 반복이 끝났으므로 low를 리턴한다.
upper bound 코드 구현
// upperBound 함수 구현
public static int upperBound(int[] arr, int target) {
int low = 0;
int high = arr.length;
while (low < high) {
int mid = (low + high) / 2;
if (arr[mid] <= target) {
low = mid + 1;
} else {
high = mid;
}
}
return low; // upper bound 위치 반환
}
이분 검색 구현(binary search implementation)
여기에 알고리즘 관련 소스코드를 구현해 놓았다.
GitHub - LimeTree0/Algorithm
Contribute to LimeTree0/Algorithm development by creating an account on GitHub.
github.com
'알고리즘' 카테고리의 다른 글
| 위상 정렬(Topological sorting) (0) | 2024.05.05 |
|---|---|
| Modular 연산에 대해 알아보자! (0) | 2023.11.27 |
| 플로이드-워셜(Floyd-Warshall) 알고리즘 (0) | 2023.08.17 |
| 순차검색(sequential search) (0) | 2022.06.23 |
| 들어가기 앞서 (0) | 2022.06.23 |