문제는 다음과 같다.
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
접근 방법
1. n개의 1로 s를 만들수 있는지 판별한다. 만약 만들 수 없다면 집합으로 표현할 수 없다.
2. s를 n으로 나눈 몫에 s를 n으로 나눈 나머지만큼 반복해서 1을 더해준다.
접근 방법 풀이
1. n개의 1로 s를 만들수 있는지 판별한다. 만약 만들 수 없다면 집합으로 표현할 수 없다.
s를 구성할 수 있는 수들중 가장 작은 수는 1이다. 그러나 1을 n번 더하여 s를 만들 수 없다면 어떤 방법으로도 만들 수 없다. 예를 들어 n=5일때 s=4이면 5개의 자연수를 가지고 4를 만들어야 한다. 그러나 자연수 n개로 구성하는 집합의 원소중 가장 작은 수는 1이고 1을 5번 더해서 4를 만들 수 없다.
2. s를 n으로 나눈 몫에 s를 n으로 나눈 나머지만큼 반복해서 1을 더해준다.
이 부분은 처음에 풀 때는 직감적으로 풀었다. 하지만 일부분만이라도 증명을 해보고 싶어 시도해봤다.
n = 1일 때:
n = 1일 때는 집합은 k 하나로만 이루어진다.
n이 1이 아니면서 s가 임의의 수 k의 p 제곱 형태로 나타낼 수 있을 때:
다음으로 s가 임의의 자연수 k, p에 대하여 s = k * p로 나타낼 때, 곱은 kp로 나타낼 수 있다. 만약 s를 ( k - q ) + k + k + ... k + k + (k + q)로 나타낸다면(q는 임의의 자연수) 곱은 (k - q)(k + q)kp - 2으로 나타낼 수 있다. kp 와 (k - q)(k + q)kp - 2를 비교해기 위해 각각을 kp - 2로 나누어주면 k2과 (k - q)(k + q)이 되고 이 둘을 비교하면 다음과 같다.
k2 > k2 - q2
그러므로 kp가 가장 크다.
n이 1이 아니면서 s가 임의의 수 k의 p 제곱 형태로 나타낼 수 없을 때:
s를 k * p로 나타낼 수 없는 경우는 산술기하평균을 이용해 구할 수 있다.(위의 경우도 산수기하평균으로 증명이 되지만 좀 더 쉬운 설명을 위해서 첨부함)
(s/n)p >= x1 * x2 * x3 * ... * xn
이때 x1, x2, ..., xn은 자연수가 되어야 되는데 s/n은 실수가 나올 수 있다. 그러면 x1, x2, ... , xn은 s/n과 가장 가까운 정수로 표현되어야 가장 큰 값을 가질 수 있다. s = 9, n = 2일 때 그래프를 보면 확실히 알 수 있다.
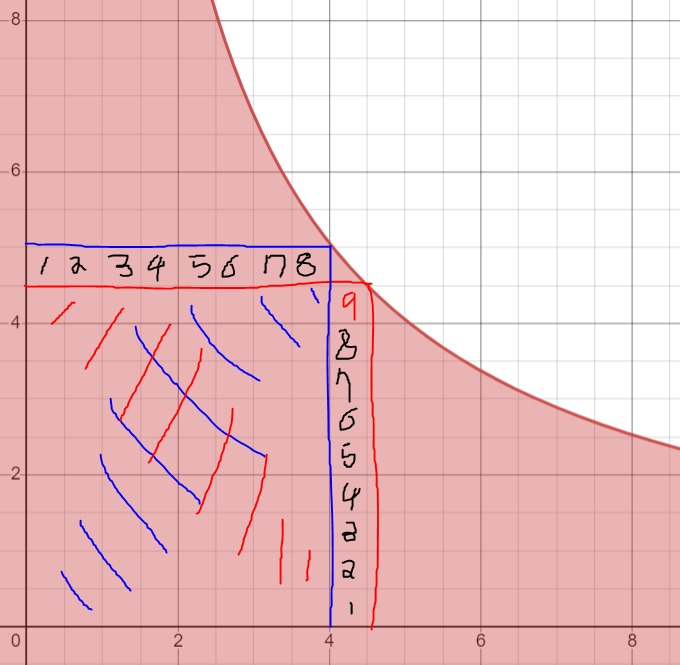
공통영역을 제외하고도 (9/2) * (9/2) = 4.5 * 4.5일 때가 가장 큰 값을 갖는데 4.5와 가장 가까운 자연수는 4와 5이다. 그리고 이때가 가장 집합의 곱의 수가 클 때이다. 즉, 각각의 숫자들이 평균값과 가까우면 가까울수록 숫자가 커진다. 평균에 가장 가까운 수를 만들기 위해 소수점을 버림해주면 그 값은 s를 n으로 나눈 몫이 되고 버림한 소수점까지 더해야 온전한 s를 얻을 수 있음으로 버림한 소수점을 모두 더한 후(s을 n으로 나눈 나머지) 이를 가장 작은 단위인 1씩 각 몫에 배분해 준다. 1씩 배분하는 이유는 평균과의 차이를 적게 하여 배분해주기 위함이다.
코드는 다음과 같다.
import java.util.*;
class Solution {
public int[] solution(int n, int s) {
// 만약 만들 수 없다면 [-1]을 반환
if(s / n == 0) return new int[]{-1};
int[] answer = new int[n];
// s÷n을 넘지 않는 가장 큰 자연수 구하기
for(int i = 0; i < n; i++) {
answer[i] = s / n;
}
// s % n의 몫을 1씩 배분
for(int i = 0; i < s % n; i++) {
answer[i] += 1;
}
Arrays.sort(answer);
return answer;
}
}