앞선 포스팅에서 Big-O표기법에 대해 간략하게 설명한 적이 있다. 여기서는 Big-O표기법에 대해 좀 더 자세한 설명과 함께 Big-O표기법을 나타내는 대표적인 함수와 여러가지 연산 규칙에 대해 설명 하려고 한다.
Big-O 표기법이란?(what is Big-O notation?)
Big-O 표기법은 알고리즘의 점근적 상한을 나타내는 표기법이다. 즉, 알고리즘이 최악의 상황에서 작동할 경우, 표기한 증가 함수와 유사한 방식으로 증가함을 나타내는 것이다. Big-O 표기법의 수학적 정의는 다음과 같다.
정의
n ≥ n0인 모든 n에 대해 f(n) ≤ c · g(n)를 만족하는 양의 상수 c와 n0가 존재하면 f(n) = O(g(n))이다.
정의를 좀 더 쉽게 이해하기 위해서 예시를 통해 정의를 설명해 보겠다. 어떤 알고리즘이 f(n) = n^3 + n^2 + 1의 성능을 갖는다고 해보자. 위에 정의를 만족하는 g(n)은 n^3이다. c = 3이고 n0 = 1일 때, 1이상인 n에 대해서 g(n)은 항상 성립한다. 그러므로 f(n) = O(n^3)이라고 표기할 수 있다. f(n)과 c · g(n)의 관계를 그래프로 그리면 다음과 같다.
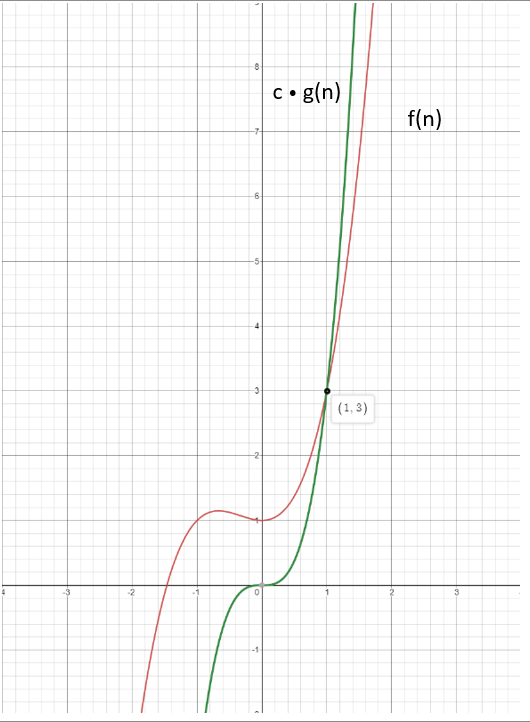
누군가는 "왜 g(n)의 식은 3n^3인데 앞에 상수없이 O(n^3)이라고 표현하나요?"라고 질문할 수 있다. 그 이유는 우리가 알고리즘을 식으로 나타내는 이유에 있다. 앞선 포스팅에서 알고리즘을 Big-O와 같은 표기법으로 나타내는 이유를 설명했다. 알고리즘을 모두 정확한 식으로 표기할 수 없기 때문에 대략적인 함수를 통해 그 성능을 비교한다. 상수의 유무가 증가하는 형태의 차이를 유의미할 정도로 크게 바꾸지 않기 때문에 상수를 제외한 가장 기본적인 함수만을 이용하여 나타낸다. 위에 그래프에서도 보듯이 함수가 증가하는 형태가 f(n), c · g(n) 모두 큰 차이를 보이지 않는다. 그렇다면 Big-O표기를 위해 사용되는 대표적인 함수는 무엇이 있는지 알아보자.
공통 시간 복잡도 함수(Common Time Complexity Function)
시간 복잡도 함수에는 알고리즘에 따라 다양하게 나올 수 있다. 하지만 알고리즘이 가지는 공통적인 부분이 있을 것이다. 이에 대한 공통 시간 복잡도를 나타내는 함수를 공통 시간 복잡도 함수(Common time complexity function)라 한다. 여기서는 아주 대표적인 함수들만 소개하겠다. 다음은 각 함수를 표로 정리한 것과 함수의 그래프이다.
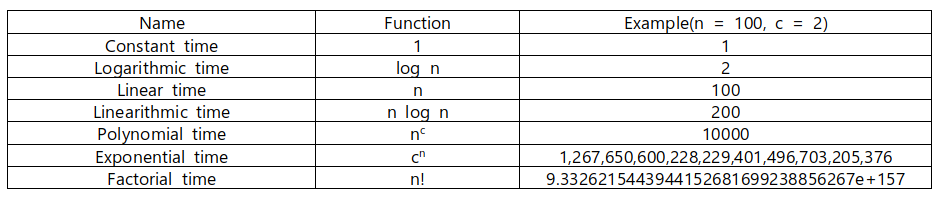
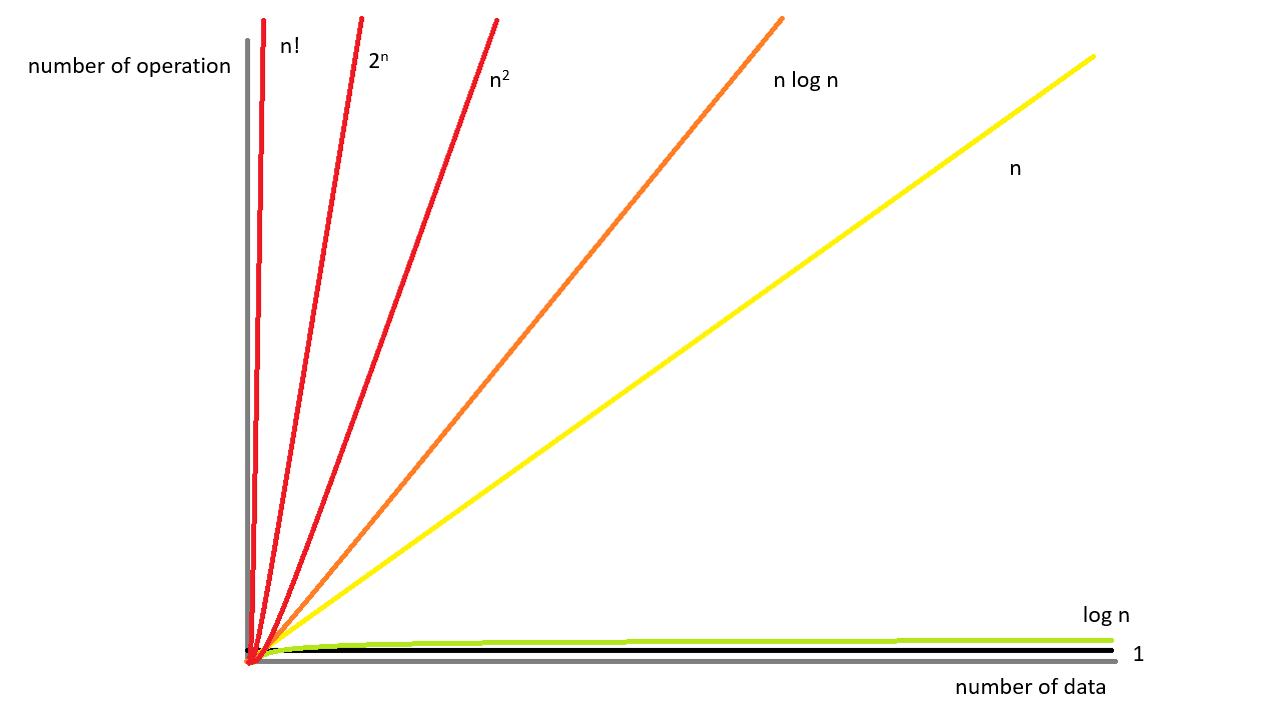
위 그래프와 표를 통해 각 함수의 증가 정도를 알 수 있다. 상수와 log n까지는 아주 좋은 알고리즘이라고 판단할 수 있다. n와 nlog n은 데이터의 양이 증가하면 많은 시간이 걸리지만 그래도 쓸 수는 있는 수준이다. 알고리즘은 아무리 느려도 n log n의 증가 형태를 가져야 쓸 수 있다. 그 이상으로 가면 계산하는데 기하급수적인 시간이 필요함으로 좋은 알고리즘이라고 할 수 없다.
Big-O 표기법 규칙(Big-O notation rules)
Big-O 표기법을 사용할 때는 몇가지 규칙이 있다.
전이성 규칙(Transitivity Rule)
전이성 규칙
f(n) = O(g(n))이고 g(n) = O(h(n))이면 f(n) = O(h(n))이다.
상수 곱셈 규칙(Multiplicative Constants Rule)
O(c · f(n) = O(f(n))이다. (상수는 무시한다.)
이 부분은 규칙이라기 보다는 Big-O 표기법 자체의 정의이기도 하다. 정의를 보면 상수는 무시하는 것으로 되어있다.
합 규칙(sum Rule)
O(f(n) + g(n)) = O(max(f(n), g(n))) = O(f(n) + g(n))이다.
이건 필자도 처음에 좀 어려웠다. f(n) = n, g(n) = n^2이라고 한다면 O(f(n) + g(n)) = O(n^2 + n) = O(n^2)이다. max(f(n), g(n)) = g(n)이기 때문에 위의 규칙이 성립한다.
곱 규칙(Product Rule)
O(f(n)) × O(g(n)) = O(f(n) × g(n))이다.
'자료구조' 카테고리의 다른 글
| 자료구조란? (0) | 2022.02.21 |
|---|---|
| 알고리즘 작성 방법 (0) | 2022.02.17 |
| 재귀 알고리즘과 반복 알고리즘 (0) | 2022.02.17 |
| 알고리즘 성능 분석 (0) | 2022.02.15 |
| 데이터를 표현하는 방법(Data representation) (0) | 2022.01.28 |