배열이란?(What is Array)
배열(array)또는 순차 리스트(sequential list)는 인덱스와 값의 쌍으로 이루어진 연속적인 메모리 위치의 집합이라고 정의할 수 있다. 배열은 인덱스와 값으로 이루어지는데 인덱스(index)는 어떤 값에 접근하기 위해 필요한 것이다. 값(value)는 배열 안에 실제로 들어가 있는 값을 의미한다. 만약 우리가 week[7] = {월, 화, 수, 목,금, 토, 일}이라는 배열을 선언한다면 요일은 배열의 값이 되고 '수'라는 값에 접근하고 싶으면 인덱스 2를 통해 접근할 수 있다. 이 부분은 c의 배열을 공부하면 배열이 어떤 식으로 작동하는지 알 수 있다.

배열은 값에 접근할 때 O(1)의 시간 복잡도를 갖는다. 즉, 배열은 어떤 값에 접근하던지 모두 동일한 시간이 걸린다. 배열이 인덱스를 참조하여 값을 접근하는 방식은 배열의 처음 주소를 기준으로 (데이터형의 크기) * (인덱스)만큼 주소를 건너뛰어서 그 값을 전달해준다. 그렇기 때문에 배열의 접근은 꼭 week[2]로 접근하는 것이 아니라 (week + 2)와 같은 방식으로 접근할 수 있다.(c의 포인터를 배우면 이해하기 쉽다.)
메모리 상의 배열과 주소 계산(Array in Memory and Address calculation)
위에서 배열을 정의할 때 메모리 위치의 집합이라고 한 부분이 있다. 이는 배열이 메모리 상에서 표현되는 방법이 메모리에 연속적으로 저장되기 때문이다. 배열이 선언되면 컴파일러는 배열의 크기만큼 연속적인 공간을 메모리에 할당한다. 그렇기 때문에 우리가 인덱스를 통해 메모리 접근이 가능한 것이다. 두 배열 int a[4] = {1, 2, 3, 4}, char b[4] = {a, b, c, d}를 메모리 상에서 표현하면 다음과 같다.
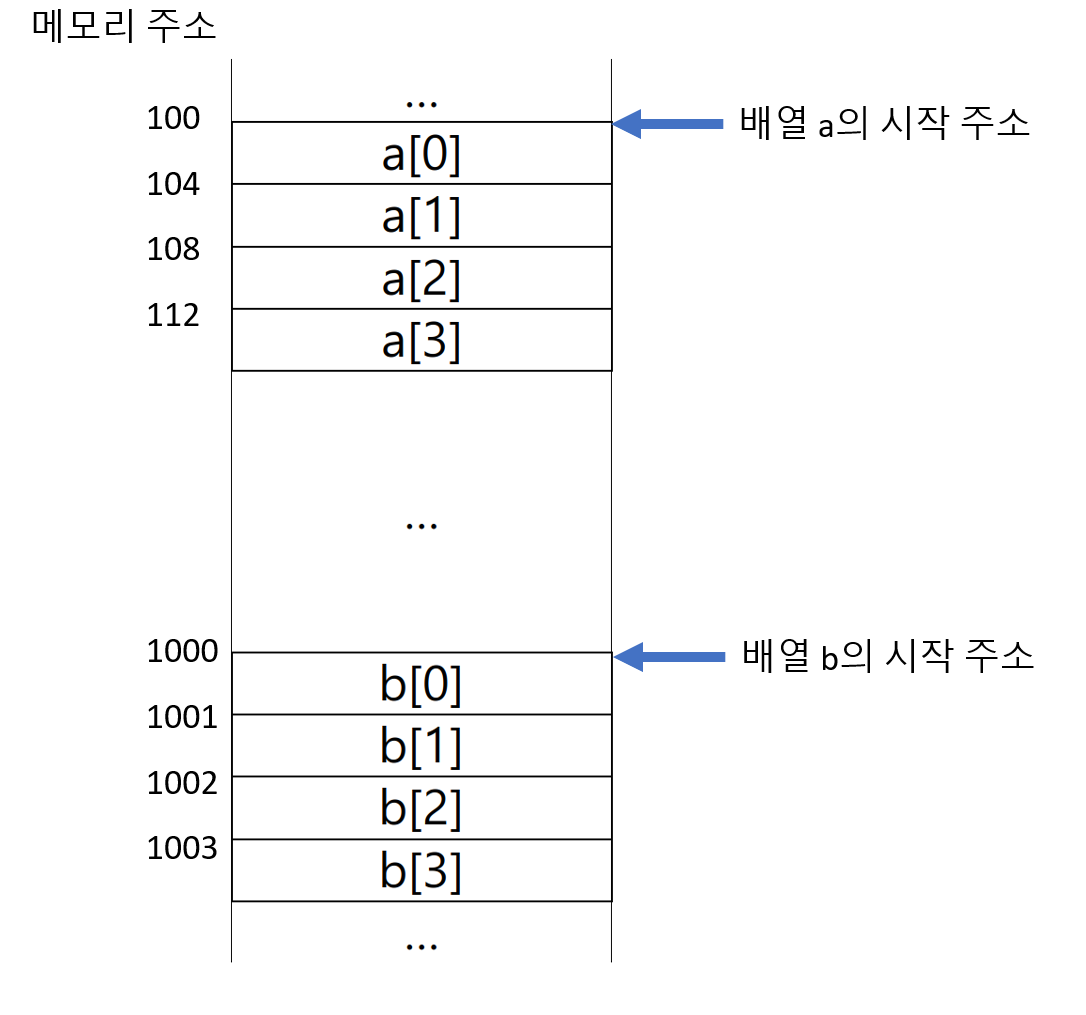
시작 주소 또는 기본 주소(base address)를 기준으로 (데이터형의 크기) * (인덱스)를 해주면 배열의 i인덱스의 주소를 알 수 있다. a[2]와 b[3]의 주소는 다음과 같다.
a[2]의 주소 = 배열 a의 시작 주소 + (데이터형의 크기) * 인덱스 = 100 + 4*2 = 108
b[3]의 주소 = 배열 b의 시작 주소 + (데이터형의 크기) * 인덱스 = 1000 + 1*3 = 1003
다차원 배열(Multidimensional Array)
앞서 우리가 다룬 배열은 1차원 배열이다. 1차원 배열도 자주 쓰이지만 시간표와 같은 형태의 데이터 시트를 만들고 싶다면 1차원 배열로는 무리가 있다. 이때 사용할 수 있는 것이 다차원 배열이다. 다차원 배열은 배열의 인덱스가 2개 이상으로 이루어진 배열을 말한다. 다차원 배열은 인덱스를 2개, 3개, 최대 n개까지 만들 수 있다. 현실에서는 2차원과 3차원 배열이 많이 쓰인다.
2차원 배열
2차원 배열은 인덱스를 2개 가지는 배열이다. 쉽게 생각하면 시간표와 같은 형태를 생각하면 된다. 우리가 표를 만들면 행(row)와 열(column)을 나누게 된다. 2차원 배열도 같은 형태로 나누어지게 된다. 2차원 배열은 다음과 같은 형태로 선언할 수 있다.
int a[2][3]
2차원 배열을 표현하는 방법에는 2가지가 있는데 행 우선순서(row major order)와 열 우선순서(column major order)가 있다. 다음은 행 우선순서와 열 우선순서로 배열 a를 나타낸 그림이다.

2차원 배열에서 주소 계산은 1차원 배열의 주소 계산과 동일한 원리이다. 단, 행 우선인지 열 우선인지에 따라 약간차이가 있다. a[m][n]이라 선언된 배열에서 원소 a[i][j]의 2차원 배열의 주소를 구하는 식은 다음과 같다.
행 우선 순서
시작 주소 + (데이터 형의 크기) * (i * n + j)
열 우선 순서
시작 주소 + (데이터 형의 크기) * (j * m + i)
3차원 배열
3차원 배열도 2차원 배열과 같은 개념으로 나타낼 수 있다. 2차원에서 1개의 인덱스를 더 추가하면 3차원 배열이 된다.
3차원 배열은 3차원 공간에 사각형 나무 조각을 차근차근 쌓아올리는 형태의 모습을 떠올리면 된다. 3차원 배열은 면우선 순서와 열 우선 순서가 있는데 이는 2차원에서 행우선와 열우선과 같은 개념이다. 주소 계산법도 2차원배열과 같은 방식으로 계산하면 된다.
'자료구조' 카테고리의 다른 글
| 큐(Queue) (0) | 2022.02.25 |
|---|---|
| 스택(Stack) (0) | 2022.02.25 |
| 자료구조란? (0) | 2022.02.21 |
| 알고리즘 작성 방법 (0) | 2022.02.17 |
| 재귀 알고리즘과 반복 알고리즘 (0) | 2022.02.17 |