트리란?(What is Tree?)
트리는 우리가 일상생활에서도 많이 볼 수 있는 형태의 자료구조이다. 윈도우 탐색기에서의 폴더 구조나 대진표가 대표적인 트리 구조이다. 트리는 나무를 거꾸로 뒤집어 놓은 형태를 가지며 노드라 불리는 데이터 요소를 기준으로 나무가지가 뻗어나가듯이 노드들이 연결되어 있다. 트리를 좀 더 명확하게 정의하면 다음과 같다.
정의
트리는 다음과 같이 재귀적으로 정의된다.
- 트리는 최상위 노드(node)인 하나의 루트(root)를 갖는다.
- 루트를 제외한 나머지 노드들은 n(n≥0)개의 서로소인 부분집합 T1, ... ,Tn 으로 분리되는데, 각각의 부분집합은 마찬가지로 트리이다. 이때, T1, ... ,Tn을 서브트리(subtree)라 한다.
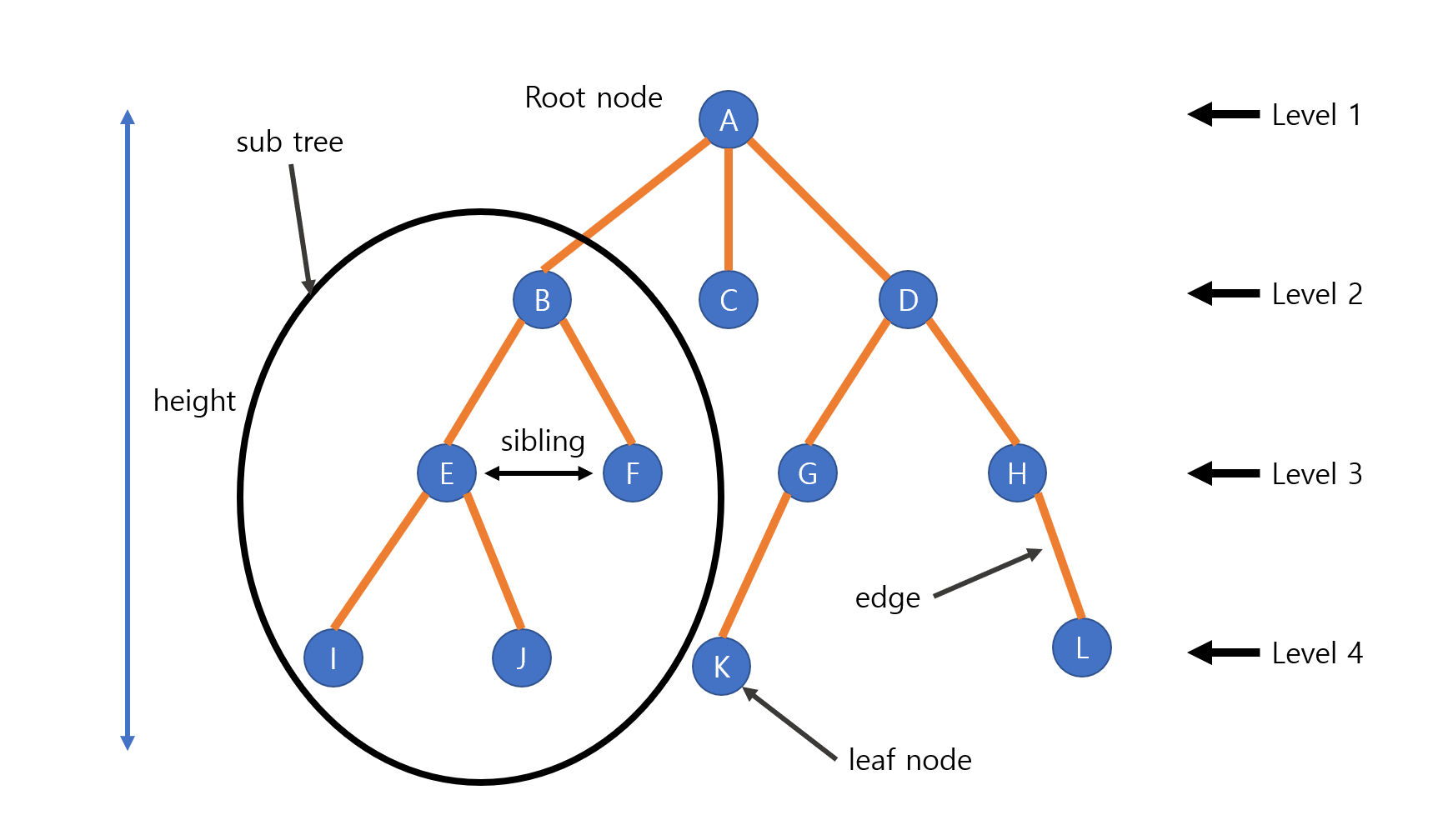
트리가 무엇인지 간단하게 알았으니 이번에는 트리의 각 요소들의 이름과 특징을 알아보기로 한다. 먼저 트리는 노드와 엣지로 표현된다. 노드(node)란 정보를 담고 있는 데이터 요소이다. 노드는 정점(vertex)라고 불리기도 한다. 그리고 이 노드들을 이어주는 선들을 엣지(edge)라고 한다. 각 노드들은 일정한 개수의 엣지를 가지는데 이 개수를 차수(degree)라고 한다. A의 경우, 3개의 엣지를 가지므로 A의 차수는 3이고, B는 2, K는 0의 차수를 가진다. 이는 노드가 가지는 서브 트리의 개수라고 바꾸어 말할 수 있다.
이번에는 노드들의 관계를 나타내는 용어를 알아보자. 먼저, 위 그림에서 G와 K 노드를 보면 서로 가깝게 연결되어 있다. 이렇게 직접적으로 연결된 노드들은 부모, 자식관계가 형성된다. 이때 G노드는 K의 부모(parent)노드가 되고 K노드는 G의 자식(child)노드가 된다. 더 확장시켜 D노드는 G의 부모노드이기도 하지만 K의 조부모(grandparent)노드가 되기도 한다. 자손(descendat) 노드는 현재 노드의 서브트리에 있는 모든 노드들을 가리키며 B의 자손 노드는 E, F, I, J가 된다. 조상(ancester) 노드는 트리의 루트에서 현재 노드까지의 경로상에 있는 모든 노드를 가리킨다. K노드의 조상은 A, D, G가 된다. 레벨(level)은 루트노드를 1레벨로 하여 루트노드를 기준으로 특정 노드의 거리를 나타낸다. 트리중 가장 높은 레벨을 트리의 높이(heigt)또는 깊이(depth)라고 한다. 위 그림에서는 트리는 4의 깊이를 갖는다.
같은 부모를 가지는 갖는 같은 레벨의 노드들끼리는 형제(sibling)라고 한다. 자식이 없는 차수가 0인 노드들을 잎(leaf)또는 단말 노드(terminal node)라고 하는데 그림에서는 C, F, I, J, K, L이 된다. 단말 노드들은 외부 노드(external node)라고 부르기도 하는데 이와 반대로 내부에 있는 노드들은 내부 노드(internal node) 또는 비단말 노드(nonterminal node)라고 한다. 서브트리(subtree)는 루트노드를 제외한 부분적인 트리를 말한다. 그림에서는 B를 루트로하는 서브트리, D를 루트로 하는 서브트리등이 있다.
트리의 종류(Types of Tree)
트리는 하나의 부모 노드에 2개 이상의 자식을 가지는 다진 트리(multiway tree)와 부모 노드가 최대 2개 이하의 자식만을 가지는 이진 트리(binary tree)로 나눌 수 있다. 다진 트리와 이진 트리의 차이점은 다음과 같다.
| 다진 트리 | 이진 트리 |
다진 트리는 하나 이상의 노드를 가져야 하며, 서브 트리의 위치는 자유롭다. |
이진 트리는 노드의 개수가 0이 될 수 있으며, 서브 트리의 위치는 왼쪽 자식과 오른쪽 자식으로명확하게 구분되어야 한다. |

다진 트리에서는 위 그림의 트리는 같은 트리이지만 이진 트리에서는 서로 다른 트리로 취급한다. 이진 트리를 정의하면 다음과 같다.
정의
이진 트리는 공집합이거나 루트와 왼쪽 서브 트리, 오른쪽 서브 트리의 두 개의 분리된 이진 트리로 구성된 노드들의 유한 집합이다.

이진 트리는 위 그림처럼 경사 이진 트리(skewed binary tree), 완전 이진 트리(complete binary tree), 포화 이진 트리(full binary tree)등이 있다.
이진 트리의 성질(Properties of Binary Tree)
이진 트리의 최대 노드 수
- 이진 트리의 레벨 i에서 가질 수 있는 최대 노드 수는 2 i - 1 (i≥1)이다.
- 깊이가 d인 트리가 가질 수 있는 최대 노드 수는 2d - 1 (d≥1)이다.
단말 노드 수와 차수가 2인 노드 수와의 관계
모든 이진 트리에 대해, 단말 노드의 수를 n0, 차수가 2인 노드의 수를 n2라 하면, 항상 다음의 식이 성립한다.
n0 = n2 + 1
정의
이진 트리의 깊이가 d일 때 총 노의 수가 2d-1(d≥0)인 이진 트리를 깊이가 d인 포화 이진 트리라 한다.
정의
깊이가 d이고 노드의 수가 n인 이진 트리의 모든 노드들과 깊이가 d인 포화 이진 트리의 각 노드들에 레벨 우선 순서로 1에서 n까지의 번호를 부여한 것이 모두 일치한다면, 이진 트리를 깊이가 d인 완전 이진 트리라 하고, 그 역의 경우도 항상 성립한다.
트리의 주요 성질
- 트리의 한 노드에서 다른 노드로 가는 경로는 유일하다.
- n개의 노드를 갖는 트리는 n-1개의 엣지를 갖는다.
- 완전 이진 트리가 n개의 노드를 갖는 경우, 이 트리의 높이는 ⌊log2n +1⌋이다.
증명 1:
트리는 사이클을 갖지 않기 때문에 위 성질이 성립한다.
증명 2:
단말 노드 수와 차수가 2인 노드 수와의 관계에서 증명
증명 3:
log22k-1 ≤ log2n ≤ log2(2k-1)
k-1 ≤ log2n ≤ log2(2k-1) < log2k - log21
k-1 ≤ log2n < log22k - log21 = k
k ≤ log2n + 1 < k + 1
여기서 2k-1은 완전 이진 트리가 높이 k일 때 가질 수 있는 최소 노드의 개수이고 2k -1는 최대 노드의 개수이다. 그리고 마지막 부등식은 바닥 함수(floor function)를 나타내는 부등식이다.
트리 구현(Tree Implementation)
구현은 아래 필자의 깃허브에 있으니 참고하길 바란다. 기본적인 원리만 구현을 했기 때문에 실제 사용에는 무리가 있다.참고만 하길 바란다. 트리 구현에 대한 자세한 설명은 추후에 포스팅하겠다.
GitHub - LimeTree0/Data-Structure
Contribute to LimeTree0/Data-Structure development by creating an account on GitHub.
github.com
'자료구조' 카테고리의 다른 글
| 스레드 이진 트리(Threaded binary tree) (0) | 2022.03.03 |
|---|---|
| 트리 순회(Tree Traversal) (0) | 2022.03.01 |
| 이중 연결 리스트(Doubly Linked List) (0) | 2022.02.25 |
| 원형 연결 리스트(Circular Linked List) (0) | 2022.02.25 |
| 단순 연결 리스트(Singly Linked List) (0) | 2022.02.25 |