쌍대(duality)
쌍대(duality)라는 것은 한 쪽에 항등원과 연산자를 바꾸면 다른 부분을 얻어 낼 수 있다. 이는 우리가 학교에서 배운 대우와 같은 개념이다. 만약 q->p라는 명제가 주어졌을 때 대우는 ~p -> ~q이다. 이를 부울 대수에서 사용하면 1 + 1 = 1일때 쌍대를 이용하면 0 · 0 = 0임을 알아낼 수 있다. 이 성질은 부울 대수에서 식을 계산할 떄 상당히 유용하므로 꼭 알아두는 것이 좋다. 부울 대수에서 쌍대를 구하는 방법은 AND 연산자와 OR 연산자를 바꿔주고 1과 0을 서로 바꾸면 된다.
기본 정리
다음 표는 부울 대수의 기본정리 6개와 공준 4개에 대한 표이다.
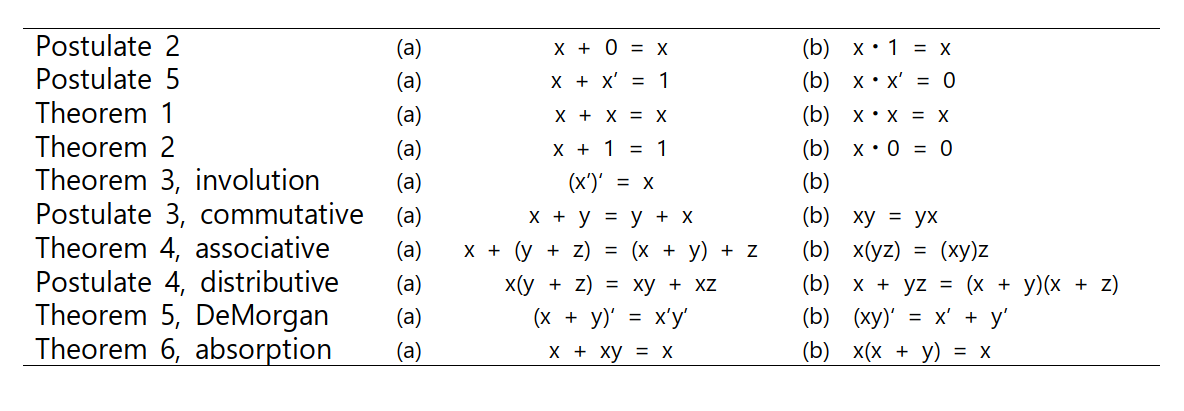
이제부터 위 표에 주어진 공준을 바탕으로 각 정리에 대해 증명을 해보도록 하겠다. 부울 대수의 공준에 대한 자세한 내용은 이전 포스팅을 참조하기 바란다. (https://limecoding.tistory.com/23)
정리 1

정리2

정리2(b)는 정리2(a)의 쌍대로 증명된다. 쌍대는 앞서 설명한 것처럼 연산자와 원소를 바꿔줌으로써 얻을 수 있다.
정리2(b)의 x는 보수를 취해도 x나 x'의 의미가 크지 않아서 그냥 x로 표기한다.
정리3
보수에 대한 정의는 공준5에서 보여주고 있다. x'의 보수는 (x')'이고 (x')'은 x와 같다.
정리4, 5
정리4와 5은 지금 증명하기가 어려운 관계로 추후 추가적인 공부를 통해 증명을 하겠다. 식의 성립 여부는 모든 경우의 수를 넣어 식의 성립을 증명할 수 있다. 이를 표로 만든 것을 진리표라고 하는데 이는 다른 포스팅에서 다루겠다.
정리6

여기서 주의해야할 점은 쌍대를 구할 때 괄호 표기를 잘해야 한다. 쌍대를 구하는 건 상수나 변수에 보수를 취하고 연산자를 바꾸는 것과 같다. 이때 x + xy에서 xy = k로 두면 x + xy = x + k이고 이것의 쌍대를 구하면 x' · k'이다 여기서 보수가 연산자 우선순위가 가장 높기 때문에 k'을 먼저 해준다. (이 식에서 x'은 x와 큰 의미가 없기에 계산하지 않는다.)
k' = x' + y'이다.(드모르간 법칙) 그러므로 x +xy의 쌍대는 x' · k' =x'(x' + y')이는 곧 x(x + y)로 나타낼 수 있다.
연산자 우선순위
연산자의 우선순위는 괄호(parentheses), NOT(complement), AND( · ), OR(+) 순이다.
(x + y)'에서 계산 순서는 괄호내의 계산식, 보수 순서로 해야 한다. AND와 OR은 각각 ×와 +로 치환한다면 보수 연산을 제외한 나머지 연산자는 일반적인 대수학에서 사용되어지는 연산자의 연산 우선순위와 같다.
'digital design' 카테고리의 다른 글
| 정준 형식과 표준 형식(Canonical form and Standard form) (0) | 2022.01.21 |
|---|---|
| 부울 함수(Boolean Functions) (0) | 2022.01.20 |
| 부울 대수의 기본 정의와 공리적 정의 (0) | 2022.01.19 |
| Digital Systems and Binary Numbers (0) | 2022.01.16 |