What is Digital System?
- Discrete information (digit number, 26letters, etc.)을 이용하여 정보를 표현하고 변경할 수 있다는 특징이 있다.
- Digital System의 이름은 원래 컴퓨터의 초기 목적인 숫자 계산을 위해 만들어 졌기 때문에 digit(숫자)를 계산하는 시스템이라는 의미로 Digital System이 되었다.
- digital System은 물리적인 요소인 signal을 통해 signal의 boltages와 currents를 변경함으로써 정보를 나타낸다.
- 오늘날에는 2개의 discrete values로 정보를 나타내는데 이를 bit라고 한다. 그리고 이 bit들이 모여 binary code를 이룬다.
Binary numbers
우리가 아는 숫자 표현방식은 156, 4576같이 표현한다. 이는 우리가 숫자를 사용하기 편리하게 표기해 놓은 것인데 숫자를 정확하게 표현한다면 다음과 같다.
4×103 + 5×102 + 7×101 + 6×100
이를 일반적인 식으로
an×rn + an-1×rn-1+... a2×r2 + a1×r1 + a0×r0 + a-1×r-1 + a-2×r-2+ ... + a-m×r-m
으로 나타낼 수 있다. 여기서 an은 coefficient를 나타내고 r은 나타나고자하는 숫자의 radix (or base) 를 의미한다.
coefficient는 r을 넘어갈 수 없다. (coefficient < r) 예를 들면 10진수에서 각자리의 숫자는 10을 넘어 가지 않는다.
위에 나타낸 4576의 coefficient는 각각 4, 5, 7, 6이고 r은 10이 되는 것이다.
만약 r이 10을 넘어가게 되면 10이상의 숫자는 알파벳을 통해 표현하게 되는데 대표적 예가 hexadecimal(base-16)이다.
hexadecimal에서 10이상이 넘어가게 되면 10~15는 각각, A, B, C, D, E, F로 대체되게 된다.
(B65F)16을 10진수로 바꾸면 11×163 + 6×162 + 5×161 + 15×160 = 46,687이 된다.
2진수의 경우에는 1과 0으로 숫자를 나타내며 r은 2가 된다. 그러므로 2진수를 10진수로 변환할 때는 1이 있는 자리의 자리수 크기만큼 더해주면 된다.
(110101)2 = 32 + 16 + 4 +1 = (53)10
또한 2진수는 컴퓨터에서 쓰이는 숫자인 만큼 컴퓨터의 저장 용량이나 데이터 전송 속도등의 표기를 위해 쓰이며 2의
n승(2 to the power of n)에 대한 표는 다음과 같다.

표에는 안나와 있지만 각각 2의 10승은 K(Kilo), 2의 20승은 M(Mega), 2의 30승은 G(Giga), 2의 40승은 T(Tera)로 되어있다. 예를 들어 4G = 232이다. 이진수의 사칙연산은 radix가 10에서 2로 바뀐 점만 유의하면 10진수 계산과 동일하다.
Number-Base Conversions
decimal를 r base-number로 바꾸기 위해서는 먼저 integer part와 fraction part로 나누어야 한다. farction과 integer 계산 방법이 따로 존재하기 때문에 이는 각각 나누어 설명할 것이다.
Integer part
정수 10진수를 r진수로 바꾸는 방법은 10진수를 r로 나누어 준다. r로 나누면 몫이 나오는데 이를 연속적으로 나눌 수 없을 때까지 계속해서 나누어 준다. 각 단계에서 나누면 나오는 나머지가 있는데 나머지를 역순으로 적으면 10진수를 r진수로 변환된 수가 나온다. 밑에 예시는 r이 2일때 예시이다. 즉 10진수를 2진수로 변환시켜준 것이다.
(작은 팁으로 2진수는 binary, 8진수는 octal, 16진수는 hexadecimal 이라고 한다.)
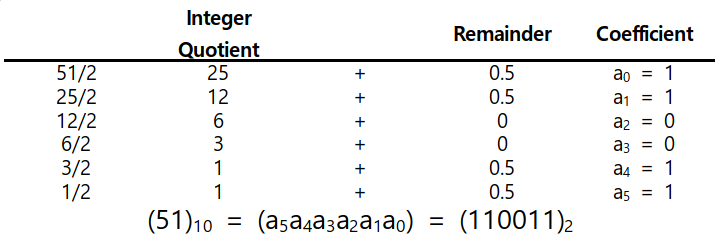
Fraction part (if it has radix point)
소수점의 경우, r을 곱함으로써 계산할 수 있다. 소수부분을 0이 될 때까지 r을 곱해준다. 소수부분에 r을 곱하게 되면, 정수부분이 0~r-1까지 나올 것이다. 이 정수는 r을 곱할 때마다 계속 나오게 되는데 이 정수를 차례대로 나열하면 소수를 r진수로 바꾼 수가 된다. 아래 예시는 10진수 소수부분을 2진수로 변환한 것이다.
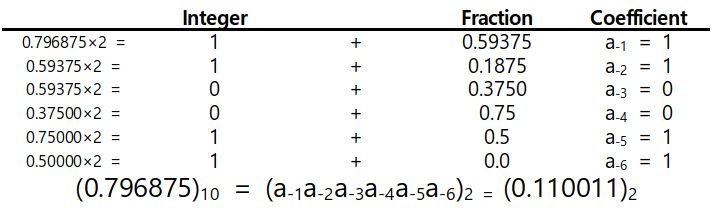
여기서 유의할 점은 정수부분의 나머지는 역순으로 나열해야하고 소수부분의 정수는 순서대로 나열해야 올바른 값을 얻을 수 있다.
정수와 소수를 모두 가지는 숫자를 2진수로 변환할 때는 정수와 소수부분을 나누고 각각 변환한 후 두 수를 더해주면 된다. 위에 예시로 든 51과 0.796875를 모두 가지는 수인 51.796875를 2진수로 변환해주면 (110011.110011)2가 된다.
Octal and Hexadecimal Numbers
2진수는 숫자의 길이가 너무 길기 때문에 사람이 알아보기에는 어려운 점이 많다. 그렇기에 자릿수를 줄이기 위한 방법으로 8진수와 16진수가 있다. 8진수는 1/3으로 16진수는 1/4로 2진수의 길이를 줄여준다. 일반적으로는 16진수를 많이 사용한다. 아래의 표는 각각의 10진수, 2진수, 8진수, 16진수가 어떻게 대응되는지를 나타내는 표이다.

2진수에서 8진수의 변환은 2진수를 3개씩 묶어서 1개의 숫자로 표현하고 16진수의 경우는 4개씩 묶어서 표현한다.
(1101 1000 1111)2 = (D8F)16 = (110 110 001 111)2 = (6617)8
으로 표현할 수 있다. 만약 숫자가 3개나 4개로 딱 떨어지지 않으면 앞자리에 0을 포함하여 계산하면 된다.
Complements of Numbers
Complements는 컴퓨터의 뺄셈 연산을 간단하게 해주거나 로직을 조작하는데 유용하다.
보수에는 2개의 보수가 있는데 하나는 radix complement와 diminished radix complement가 있다. 이는 각각 r의 보수와 (r-1)의 보수로 불리기도 한다.
Diminished Radix Complement
n자리로 표현된 r진수 N이 주어졌을 때, (r-1)의 보수는 (rn-1)-N으로 표현할 수 있다. 밑에 예시를 들겠다.
The 9's complement of 765124 is 999999 - 765124 = 234875
The 9's complement of 065124 is 999999 - 765124 = 934875
이 내용을 binary number에 적용하면 r = 2이기 때문에 (2n - 1) - N으로 나타낼 수 있다. N에서 각 자리수의 계산은 1-0 = 1 or 1-1 = 0이기 때문에 각자리의 숫자를 0에서 1로, 1에서 0으로 바꿔 줌으로써 1의 보수를 얻어낼 수 있다.

Radix Complement
radix complement는 r의 보수(r's complement)라고도 불리며 rn-N으로 표현할 수 있다. r의 보수는 (r-1)의 보수에서 1을 더해서 얻을 수 있다. 그 이유는 다음과 같다. (r-1)의 보수에 1을 더한다는 것은 다음과 같은 식으로 나타낼 수 있다.
rn - N = [(rn - 1) - N] + 1 = (rn - 1 + 1) - N
또다른 방법은 어떠한 숫자가 주어졌을 때, 숫자의 가장 오른쪽에서부터 처음으로 만나는 0이 아닌 숫자는 r에서 빼고 나머지는 r-1에서 빼면 r의 보수가 된다. 예를 들면 9546200이라는 숫자에 10의 보수를 취하게 되면 가장 오른쪽에 00은 그대로 두고 10에서 2를 빼고 나머지 9, 5, 4 ,6은 9에서 뺀다. 그리고 그 결과값을 순서대로 나열하면 0453800이 된다.
검산은 두숫자를 더하여 1뒤에 n개의 0이 오는지 확인하면 된다.
the 10's complement of 9546200 is 0453800
the 10's complement of 0452178 is 9547812
이진수도 똑같은 방법을 적용하면 된다. 2의 보수의 경우는 비슷하지만 조금 다른 점이 있다. 앞선 10의 보수의 경우는 처음만나는 0이 아닌 수에서 10을 뺐지만 2의 보수의 경우, 처음 만난 0이아닌 수 즉, 1까지 그대로 두고 그 다음 수부터 1은 0으로 0은 1로 바꾸어 주면 된다. 처음 만나는 0이 아닌 수는 2 - 1의 계산을 하게 되는데 이는 곳 1이기 때문에 바꾸지 않아도 된다. 이후의 수는 1에서 해당 자리에 있는 수를 빼는 것이기 때문에 여기부터는 1의 보수를 만드는 것과 동일한 방법으로 진행된다.
2's complement of 110100100 is 001011100
2's complement of 110100111 is 001011001
만약 소수점이 있는 경우에는 소수점을 일시적으로 제거한 후 보수화를 시킨다. 보수화가 끝나면 소수점을 원래자리로 돌려놓는다. 예를 들면 100110.001이라는 2진수가 있다. 이를 2의 보수로 보수화하기 위해선 먼저 소수점을 없앤다. 그러면 100110001이 된다. 2의 보수를 취하면 011001111이 된다. 그리고 소수점을 원래자리에 다시 돌려 놓으면 011001.111이 된다.

보수화된 수에 다시 보수를 취하면 그 수는 원래 수와 같게 된다. 주의할 점은 r의 보수로 보수화된 수는 r의 보수를 취해야 하고 (r-1)의 보수로 보수화된 수는 (r-1)의 보수를 취해야 원래 수를 구할 수 있다.
Subtraction with Complements
우리가 일반적으로 종이와 펜으로 뺄셈을 할 때는 만약 minuend digit이 subtrahend digit보다 작으면 우리는 윗 자리에서 1을 빌려오는 방식으로 계산을 하게 된다. 하지만 디지털 하드웨어에서는 그러한 방법은 구현하기도 어려울뿐더러 구현하더라도 상당히 비효율적인 방식의 계산이 된다. 그래서 디지털 하드웨어에서는 보수를 이용하여 뺄셈 연산을 구연한다. 임의의 r진수 숫자 M과 N이 주어졌을 때, M-N의 계산 로직은 다음과 같다.
- N에 보수를 취해준 뒤, M에 N을 더한다. 수식으로는 M + (rn - N) = M - N +rn 이 된다.
- 만약 M ≥ N인 경우, end carry가 발생하는데 end carry를 없앤 나머지 수가 계산 결과가 된다.
- 만약 M ≤ N인 경우, end carry를 발생시키지 않으며 그 자체가 결과값이 된다. 만약 negative sign을 가지는 수로 표현하기 위해서는 r의 보수를 취해 얻은 결과값에 negative sign을 표시해주면 된다.
10의 보수를 이용한 뺄셈은 다음과 같다.


여담으로 컴퓨터에서는 -부호를 종이에서 쓰는 것처럼 나타낼 수 없다. 그러므로 컴퓨터를 설계할 때 미리 음수에 대한 표현을 약속하고 표현하게 되는데 이는 밑에서 다루도록 하겠다.
2의 보수를 이용한 뺄셈은 다음과 같다.


2의 보수를 이용한 뺄셈 또한 10의 보수와 비슷한 방식으로 진행된다.
1의 보수를 이용한 뺄셈은 다음과 같다.


필자도 이 부분을 처음 봤을 때 약간 헷갈렸기 때문에 혹시나 같은 상황에 있는 사람들이 있다면 이해하는데 도움이 되길 바란다.
첫 번째 계산을 보면 1의 보수를 취한 뒤, end carry를 없애고 End-around carry를 더해준다. 이는 우리가 end carry를 없애는 과정에서 생기는 문제인데 위에 과정을 수식으로 나타내면 다음과 같다.
임의의 r진수 M, N이 주어졌을 때, (r-1)의 보수를 이용한 M - N은 다음과 같다. (M ≥ N)
M - N = M + [(rn-1) - N] - rn + 1
위에 식을 설명하기 위해서 X와 Y을 각각 M과 N로 대체하고 r = 2라 한다면, M + [(rn - 1) - N]는 1의 보수를 취하는 과정인데 여기서 M ≥ N인 경우, end carry가 발생하여 우리는 이를 없애기 위해 rn을 빼 주었다. 하지만 M - N의 식을 만족하기 위해서는 (rn - 1)을 더해주어야 되는데 편의를 위해 rn을 빼 주었기 때문에 1이 모자라게 된다. 그렇기 때문에 M - N의 식을 만족하기 위해서는 1을 더해 주어야 한다.
end-around carry를 이용하지 않고 위에 주어진 식을 계산하면 10100100 - 1111111을 하는 방법이 있다. 하지만 이는 컴퓨터가 추가적인 뺄셈 계산을 해야 하기 때문에 end carry를 없애는 방법보다 비효율적일 수 있다. (컴퓨터가 계산할 때 end carry가 나오면 over flow가 발생되어 end carry는 무시하고 계산할 수 있기 때문이다.)
두 번째 계산은 우리가 임의적으로 더하거나 뺀 수가 없기 때문에 negative sign을 가지는 음수를 표현하기 위해선 1의 보수를 취해준 뒤, negative sign을 붙여주면 된다.
※end-around carry는 1의 보수 덧셈을 할 때 MSB를 넘어가는 캐리가 생길 경우 이를 다시 LSB로 전달해줘야하는데 이게 앞에 있는게 뒤로 다시 돌아오는 모양새에서 end-around carry라 불린다.
Signed Binary Numbers
우리가 일반적으로 숫자를 나타낼 때는 양수는 +부호를, 음수는 -부호를 통해 양수와 음수를 표현한다. 하지만 컴퓨터는 1 또는 0으로만 표현해야 되는 한계가 있어 음수와 양수 또한 1과 0으로 표현하게 되는데 일반적으로는 가장 왼쪽에 있는 비트(Most Significant Bit)를 음수면 1로, 양수면 0으로 표현한다. 하지만 MSB(Most Significant Bit)가 1이라고 해서 항상 음수인 것은 아니다.
컴퓨터에 저장되는 정보는 1과 0이 나열된 것이기 때문에 우리는 이 정보를 어떻게 해석할 것인가를 정해야 한다. 숫자의 경우, 부호가 없는 수(unsigned digit)인지 부호가 있는 수(signed digit)인지에 따라 가장 왼쪽에 있는 비트(MSB)가 가지는 정보가 달라진다. 부호를 가지는 수의 경우, MSB는 부호를 나타내며, 부호가 없는 수의 경우는 해당 자리의 크기만큼의 정보를 나타낸다. 예를 들면, 아래에 숫자가 unsigned digit이면 203을 나타내고 위에 숫자가 signed digit이면 부호-절대값으로 -75를 나타낸다.

우리가 음수를 나타내는 방법에는 signed-magnitude(부호-절대값), signed-1's-complement(부호가 있는 1의 보수), signed-2's-complement(부호가 있는 2의 보수)가 있다.
부호-절대값 표현은 위에서 예시를 든 것과 같이 MSB는 부호를 나타내고 나머지 비트들은 magnitude를 나타낸다. 쉽게 말해서 우리가 -75를 나타내는 것처럼 MSB는 -를 의미하고 1001011은 실질적인 수의 크기(여기선 75)를 나타낸다.
각각 부호가 있는 1의보수와 2의 보수는 우리가 앞서 뺄셈을 할 때 보수화 취하는 것처럼 양수를 보수화하면 그것이 음수가 된다. 위에 있는 11001011을 예시로 들면 11001011이 1의 보수면 10진수로 -52를 나타내고 2의 보수면 -53을 나타낸다. 다른 예시로 -12를 3가지 방법으로 나타내면 다음과 같다. (8비트로 표현)
signed-magnitude representation: 10001100
signed-1's complement representation: 11110011
signed-magnitude representation: 11110100
다음의 표는 4비트 수를 3가지 방법으로 표현한 표이다.

일반적으로 컴퓨터에서는 2의 보수를 통해 음수를 나타낸다. 컴퓨터에서 음수를 표현한다고 했을 때 부호-절대값의 경우는 부호부분과 수를 나타내는 부분을 따로 컨트롤해야 한다. 이는 컴퓨터에 더 많은 회로를 집어넣어야 한다는 단점과 그로 인해 가격이 비싸지는 단점이 동시에 발생된다. 또한 다른 방법에 비해 비교적 연산량이 많아질 수 있다. 부호 비트와 실제 수를 나타내는 비트를 따로 계산한 뒤 합쳐야 하기 때문이다.
1의 보수의 경우는 부호-절대값보다는 나은 방법이지만 여전히 문제점을 가지고 있다. 앞서 설명한 1의 보수 뺄셈의 경우도 end-around carry를 더해주는 방식으로 뺄셈을 했다. 이처럼 수를 계산하는데 있어 약간에 과정이 추가되기에 좋은 방법은 아니다. 하지만 논리 회로에서는 1을 0으로, 0을 1로 바꾸는 계산을 필요로 하기 때문에 이 부분에서는 유용하게 쓰일 수 있다.
2의 보수의 경우는 다른 표현 방법과 다르게 0은 하나로만 표현되어 같은 비트 수를 가지고도 더 많은 양의 정보를 표현할 수 있으며(1의 보수와 부호-절대값은 0을 두 개로 표현하지만 사용할 때는 둘 중 하나를 정해서 사용한다.) 2의 보수를 취한 수는 산술 연산에도 다른 추가적인 연산을 필요로 하지 않기 때문에 여러가지로 이점이 많다. 인텔 cpu가 2의 보수를 사용하는 대표적인 cpu이다.
Arithmetic Addition
일반적으로 우리가 사용하는 signed-magnitude system에서의 산술 계산은 부호와 숫자부분을 따로 계산하게 된다.
부호가 같으면 두 수를 더하고 공통 부호를 붙여준다. 부호가 다르면 큰 수에서 작은 수를 빼 주고 큰 수의 부호를 따라간다. 예를 들면 (+23) + (-54) = -(54 - 23) = -31과 같이 계산할 수 있다. 이 경우 컴퓨터 내부에서는 부호와 수의 크기를 비교하는 부분과 덧셈이나 뺄셈을 수행하는 부분이 필요하다.
signed-2's-complement는 signed-magnitude system과는 다르게 부호를 비교하거나 수의 크기를 비교하는 부분이 필요가 없다. 오직 덧셈만 하면 되기 때문이다. 덧셈 과정에서 나오는 부호 비트의 캐리는 무시하면 된다.

위에 예시에서 4번째 식을 계산하면 자리 수를 넘어가는 일이 생기는데 이를 "오버 플로우가 났다(overflow occurs)"라고 말한다. 오버 플로우는 컴퓨터의 구조적인 문제에서 발생하는 현상인데 컴퓨터는 일정한 저장 공간을 가지고 있다. 그렇기에 계산 결과가 저장 공간의 크기를 넘어버리면 넘어간 크기만큼의 정보를 잃어버리게 된다. 이는 저장공간을 확장시킴으로써 해결할 수 있지만 이 또한 한계가 있기에 이 부분은 컴퓨터 설계시 중요한 부분이 된다.
Arithmetic Subtraction
signed-2's-comlpement의 특성상 뺄셈 또한 덧셈과 같은 방법으로 변환할 수 있다. 우리는 앞서 양수에 2의 보수를 취하면 음수가 된다는 사실을 알고 있다. 그러면 음수에 보수를 취하면 어떻게 될까? 다시 양수로 돌아오게 된다. 이를 뺄셈에 적용시키면 다음과 같다.
(±A) - (-B) = (±A) + (+B)
(±A) - (+B) = (±A) + (-B)
컴퓨터는 뺄셈과 덧셈을 구분할 필요없이 덧셈은 두 수를 더하고 뺄셈은 subtrahend에 보수를 취해준 뒤 두 수를 더해주면 된다. 즉, 컴퓨터는 1가지의 회로를 가지고 2가지의 연산을 할 수 있는 것이다. 하지만 주의할 점은 결과값이 unsigned인지 signed인지에 따라 다르게 해석되야 하며 이는 프로그래머의 몫이다.
Binary Codes
디지털 시스템은 숫자도 나타내지만 현재 상태와 같은 정보를 나타내기 위해 2진화된 코드를 사용한다. 이는 컴퓨터가 2진수 체계를 따르기 때문에 그 정보도 2진수로 표현된다. 이진 코드는 비트 수에 따라 표현할 수 있는 정보의 양이 다른데 n-bits binary code의 경우, 0부터 최대 2n - 1까지 나타낼 수 있다. 그리고 각각의 코드는 고유의 정보를 나타낸다. 신호등을 예로 들면 빨간불이면 멈추고 초록불이면 갈 수 있다. 그런데 빨간불이 '가다'와 '멈추다'의 의미를 동시에 가지고 있거나 빨간불과 초록불이 모두 '가다'의 의미를 가지게 되면 그 의미가 정확히 전달되지 않는다.
Binary-Coded Decimal Code
2진화된 10진수는 2진수로 10진수를 나타내는 방법이다. 10진수에서 단일 자리는 0~9까지 총 10가지를 표현해야 한다.
그럼 여기서 문제!
10가지의 수를 표현하려면 총 몇 비트가 필요할까?
24 = 16이 필요하다. 그럼 4비트를 이용하여 0부터 9까지 표현할 수 있다. 그러면 여기서 궁금증 하나가 생긴다.
나머지 6개 2진수로 표현되는 10부터 15까지는 어떻게 되는가?
답은 '쓰지 않는다' 이다. 10개만 사용하기 때문에 그 이외에 숫자는 필요하지 않다.
0~9까지의 수는 2진수와 동일하지만 그 이후에 나오는 수는 사용하지 않는다. 우리는 이러한 이진 코드를 Binary-Coded Decimal Code라 하며 줄여서 BCD code라고 한다. BCD를 나타낼 때는 각 자리 당 4비트를 차지하기 때문에 n자리 수를 가지는 10진수는 총 n*4비트가 필요하다. 예를 들어 173이 있다면 BCD코드르 0001 0111 0011로 표현할 수 있다. 아래는 BCD코드와 BCD코드가 가지는 값을 표로 나타낸 것이다.

그런 2진수와 비교해보면 약간의 효율성이 떨어지는 부분을 볼 수 있다. 위에 예시에서 든 173의 BCD코드는 총 12비트를 사용하는 반면 2진수로 변환하면 1010 1101으로 8비트면 사용하면 표현할 수 있다. 그렇다면 컴퓨터는 효율을 중요시하면서 왜 우리는 이런 비효율적인 코드를 쓰는가?
이유는 컴퓨터의 측면에서의 효율이 아닌 사용자의 측면에서의 효율성을 따지기 때문이다. 일단 컴퓨터의 사용자는 인간이다. 인간은 2진수보다는 10진수에 더 익숙하기 때문에 컴퓨터 사용을 위해 2진수 체계를 따로 배우는 건 어떻게 보면 상당이 비효율적이다. 그러므로 인간이 사용하기 편하게 2진수 체계에서 10진수로 표현하는 BCD코드를 사용한다.
BCD Addition
BCD코드에서 덧셈을 해보자. 우리가 고려해야 될 상황은 BCD코드는 0000~1001까지 나타낸다는 것! 그렇다면 1010을 넘어서는 부분을 어떻게 처리할지가 관건이다. 여기서 우리는 머리를 살짝 써 볼 거다. BCD코드는 총16개중 10개만을 사용한다. 그렇다면 1010이 되면 6개만큼 밀어내고 한 자리 올려준다. 즉 10이 넘어가면 BCD코드 6을 더해주고 한 자리 올려준다. 각 자리에서 나올 수 있는 총합은 9 + 9 + 1(carry)= 19이기 때문에 carry는 최대 1까지 나온다. 아래는 BCD코드 덧셈하는 예시이다.

위 예시를 보면 2진수의 덧셈과 상당히 유사한 면을 볼 수 있다. BCD코드도 2진수의 덧셈과 같은 방법으로 계산하되, 그 결과값이 10을 넘어가면 6을 더해줌으로써 보정을 한다. 아래는 n-digit unsigned BCD를 계산한 예시이다.

Decimal Arithmetic
BCD코드도 2진수에서의 산술계산과 같은 방식으로 계산할 수 있다. 대신 2진수에서의 뺄셈은 2의 보수를 취해줬지만 BCD코드에서는 10의 보수를 취해준다. 뺼셈의 예시는 다음과 같다.

2진수에서 MSB (Most significant bit) 가 1이면 음수, 0이면 양수였다. BCD코드에서는 9면 음수, 0이면 양수로 표현한다. 위에 예시는 293에서 697을 빼는 과정이다. 단지 덧셈과 다른 점은 subtrahend에 10의 보수를 취해준 뒤 더해주는 과정이 추가되었다. 결과값은 10의 보수가 취해진 형태이다. 만약 -404와 같은 형태로 바꾸고 싶다면 결과값에 10의 보수를 취해준 뒤 앞에 -기호만 붙여주면 된다.
Other Decimal Codes
10진 코드에는 여러가지 코드가 있는데 우리는 코드를 크게 weighted code와 non-weighted code로 나눌 수 있다.
weighted code는 1이 어떠한 값을 가지고 있는 것이다. 이진수나 BCD코드가 weighted code에 속한다.
다음은 weighted code의 예시이다.

각 코드에 대해 설명하면 BCD코드는 각 자리가 나타내는 가중치가 8421이라서 8421 코드라고도 불리며, 특징은 앞서 다룬 내용과 같다. 2421 코드는 가중치가 2421이기 때문에 2421코드라 불리며 재미있는 특징은 2421코드로 4를 나타낼 때 0100과 1010 2가지 방식으로 표현할 수 있다. 하지만 두 가지 모두 유효하지 않게 1가지만 정하여 사용해야한다.
84-2-1코드 또한 비슷한 이유로 이름이 붙었다.
다음은 non-weighted code로 각각의 자리가 어떤 값을 갖지는 않지만 일련의 1과 0이 모여 어떤 패턴을 만들었을 때 해당 패턴이 어떤 고유한 값을 가지는 것을 말한다. 쉽게 말하면 ㄱ, ㄴ, ㄷ이 따로 있으면 아무런 의미가 없지만 가수, 나라, 다람쥐같이 글자들이 모여 하나의 의미를 가지는 무언가를 만드는 게 비가중치 코드이다. ㄱ, ㄴ, ㄷ이 1과 0 역할이고 이 1과 0이 110 0001으로 배열되면 아스키코드로 소문자 a가 되는 형식이다. 비가중치 코드에는 excess-3코드, ascii코드, gray코드등이 있다. 다음은 excess-3코드와 gray코드표이다.

ASCII Character Code
아스키코드는 American Standard Code for Information interchange의 약자로 미국이 정보통신을 위해 만든 미국 표준 코드이다. 아스키코드는 총 7비트로 이루어져 있으며 8비트를 사용하는 경우는 패리티 비트나 이탤릭체 변환 등의 다양한 방법으로 사용된다. 다음은 아스키코드표이다.

문자를 제외한 나머지는 통신제어나 프린트에 사용되는 제어문자이다.
Error-Detecting Code
아스키코드는 총 7비트를 이용하여 표현할 수 있지만 컴퓨터는 보통 4, 8, 12와 같은 형식으로 비트를 나누어 사용한다.
아스키코드는 컴퓨터에서 8비트를 이용하여 나타내는데 이때 가장 왼쪽의 비트를 오류를 검출하는데 사용한다. 오류를 검출하는 방법은 7비트에서 1의 개수가 몇개인지를 판단하여 가장 왼쪽의 비트를 정한다. 만약 8개의 비트를 모두 짝수로 맞추면 이를 even parity(짝수 패리티)라 하고 홀수로 맞추면 odd parity(홀수 패리티)라 한다. 일반적으로 짝수 패리티가 많이 사용된다. 아래는 짝수 패리티와 홀수 패리티의 예시이다.

패리티 비트는 아스키코드를 보낼 때 같이 보내진다. 그러면 데이터를 받는 쪽에서 짝수 패리티인지 홀수 패리티인지에 따라 검사를 한다. 이상이 없다면 이상이 없다고 보낸 쪽에 알려주고 오류가 났다면 보낸 쪽에 다시 전송을 요청한다.
패리티 비트에서의 오류는 보낼 때 1의 개수와 받을 때 1의 개수가 다른 상태를 말한다. 예를 들어 짝수 패리티에서 보낼 때 짝수 개의 1을 보냈는데 받을 때 1의 개수가 홀수면 오류가 생긴 것이다. 하지만 여기서 문제점은 1의 개수가 짝수 개가 들어왔지만 2개의 1이 누락됐다면 오류 검출이 힘들게 되는 단점이 있다. 예를 들자면 01000010을 보냈지만 받았을 때 00000000이 들어와도 패리티 검사에서는 오류 검출이 되지 않는다.
Binary Storage and Registers
Register
비트들은 2진셀(binary cell)에 저장되며 각 셀들은 1개의 비트를 저장하며 외부의 신호에 따라 0과 1을 저장하고 내보내는 역할을 한다. 이 이진 셀들이 모여서 레지스터(register)가 된다. 레지스터의 정보는 n-tuple로 나타낼 수 있다. 레지스터에 저장된 정보들은 어떻게 해석하느냐에 따라 비트가 의미하는 정보가 변할 수 있다. 예를 들어 어떤 8비트 레지스터에 1100 0110이라 저장되어 있다가 가정해보자. 앞서 배운 ASCII코드와 짝수 패리티를 가지는 문자라고 한다면 우리는 이를 문자 F라고 해석할 수 있다. 부호가 없는 2진수로 해석하면 198이 되고 부호가 있는 2의 보수 2진수로 해석하면 -58이 된다. BCD코드로 해석하면 해석이 되지 않는다. 앞 4비트가 1001을 넘어가기 때문이다. 이처럼 레지스터 안의 정보는 어떤 특정한 정보가 저장된 게 아니라 이 비트들을 어떻게 해석하느냐에 따라 다른 정보가 되는 것이다.
Register Transfer
우리가 컴퓨터를 사용할 때 어떻게 키보드에서 컴퓨터로 문자가 입력되는지 알아보자.

먼저 우리가 컴퓨터에게 정보를 전달하기 위해서는 입력장치가 필요하다. 입력장치는 키보드나 마우스와 같은 것들이 될 수 있다. 여기서 입력장치는 키보드이다. 그러면 우리는 키보드로 'unit'이라는 글자를 입력한다. 그럼 중간에서 입력을 제어하는 컨트롤 장치가 적절하게 제어해서 input register에 정보를 저장한다. cpu에서는 input register에 데이터가 있는지 판단하고 있다면 가져와서 processor register에 저장한다. 이 과정을 processor register가 다 찰 때까지 하는데 processor register는 입력순서를 유지하기 위해 계속해서 한 칸씩 옆으로 밀어낸다. processor register이 다 차면 cpu는 Memory Register에 processor register의 정보를 전송한다. 그러면 짝수 패리티를 이용하는 아스키코드 4글자가 저장되게 된다. 여기서 비트들을 저장하는 역할을 하는 곳이 있는데 이게 바로 레지스터이다.
'digital design' 카테고리의 다른 글
| 정준 형식과 표준 형식(Canonical form and Standard form) (0) | 2022.01.21 |
|---|---|
| 부울 함수(Boolean Functions) (0) | 2022.01.20 |
| 부울 대수의 기본 정리와 성질 (0) | 2022.01.19 |
| 부울 대수의 기본 정의와 공리적 정의 (0) | 2022.01.19 |