개요
부울 함수는 2진 변수, 상수 0과 1, 그리고 논리 연산 기호로 나타낼 수 있다. 부울 함수는 결과값으로 0 or 1을 갖는다.
우리는 부울 함수를 다양한 방법으로 나타낼 수 있다. 우리가 익숙한 대수적인 표현으로 나타낼 수도 있고 회로도를 통해 나타낼 수도 있으며 진리표를 통해 나타낼 수도 있다. 그러면 다음에 주어진 식을 각각의 방법으로 나타내 보겠다.
F1 = (x + y)(x + y')
진리표(Truth table)
진리표는 각각의 변수가 가지는 값에 대해서 어떤 결과값이 나오는지를 모두 적어 놓은 표이다. 진리표의 행(row)의 개수는 2n개이고 열(column)의 개수는 (변수의 개수) + (해당 변수로 이루어진 함수의 개수)이다. 만약 x, y, z로 이루어진 함수가 2개가 있다면 행의 개수는 8개이고 열의 개수는 5개가 된다. 그러면 위에 주어진 F1을 진리표로 나타내 보겠다.
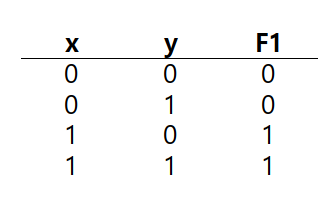
여기서 눈썰미가 좋은 사람들은 표에서 재미있는 사실 하나를 찾을 수 있다. x와 F1의 값을 자세히 보면 y값과 상관없이 서로 같은 값을 나타내고 있다. 즉 F1의 값은 결국 x의 값이라고 표현할 수 있다는 말이다. 이러한 특징들을 잘 찾아내면 실제 회로를 만들 때 아주 편리하다.
회로도(Logic-circuit diagram or Schematic)
회로도는 위에 진리표보다 좀 더 보기편하고 궁극적으로 우리가 만들려는 것은 회로이기에 회로의 전체적인 모습을 파악할 수 있다. 보통 회로도는 그 자체로 바로 얻어 지기보다는 진리표나 대수적 표현을 한번 거쳐서 표현된다. 그러면 위에 주어진 식을 이용해 회로도로 표현해보도록 하겠다.
먼저 x, y 가 각각 0, 0 일 때와 1, 0일 때, 1, 1일 때를 보면 마치 x + y와 같은 형식으로 결과값이 나오는 것을 볼 수 있다. 이를 통해 회로에는 OR게이트가 들어간다는 것을 유추할 수 있다. 그런데 0, 1일 때는 OR게이트방식으로 작동하지 않는다. 그러면 x, y가 0, 1을 가질 때 x + y를 0으로 만들어주는 다른 무언가가 필요하다. x + y = 1일 때 이를 0으로 만드는 것은 1 · 0을 하는 것이다. x + y'는 x, y가 0, 1일 때 0이 되어 F1의 값을 가질 수 있게 해준다. 그 이외에 상황에서는 영향을 주지 않는다. 그러므로 우리에게 필요한 건 2개의 OR게이트와 1개의 AND게이트 그리고 1개의 NOT게이트이다. 이를 조합하면 다음과 같다.
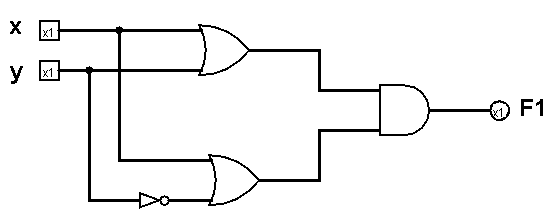
우리는 앞서 진리표에서 x와 F1의 값이 같다는 걸 알아냈다. 이를 회로도에 적용시키면 다음과 같다.
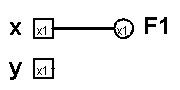
위 회로도와 아래 회로도의 차이점이 보이는가? 위 회로도에는 2개의 OR게이트, NOT게이트와 AND게이트가 각각 1개씩 사용된 반면, 아래의 회로도는 어떠한 게이트도 사용되지 않았다. 아래 회로가 한눈에 봐도 간단해 보일 뿐 아니라 만들기도 쉬워 보인다. 이처럼 같은 동작을 하는 회로를 여러가지 방법으로 만들어 낼 수 있다. 공학자는 이러한 여러 회로 중에서 만들기 쉬우면서 값도 싸지만 우리가 원하는 동작을 하는 회로를 찾을 수 있어야 한다.
대수적 표현과 조작(Algebraic expression & Manipulation)
대수적 표현은 우리가 수학에서 함수를 식으로 표현하는 방식을 말한다. 즉 F1 = (x + y)(x + y') 이 자체가 대수적 표현이다. 앞서 설명한 진리표와 회로도로도 표현할 수 있지만 이걸 가지고 다양한 회로도를 만들기는 상당히 어렵다. 그래서 회로도를 만들거나 진리표를 만들 때는 주로 대수적인 표현을 사용한다.
부울 함수에서 각 항에 있는 변수는 literal (리터럴)이라고 한다. F1함수는 4개의 리터럴과 3개의 연산자, 그리고 4개의 항을 가지고 있는 부울 함수이다. (항 or term이란 문자나 숫자의 곱으로 나타내지는 한 덩어리를 말한다. xy + x'y'은 2개의 항과 4개의 리터럴 그르고 1개의 연산자를 가진다.) 부울 함수에서 연산자는 회로도로 표현할 때 AND연산자는 AND게이트로 OR연산자는 OR게이트로 표현할 수 있다.
우리가 앞에서 F1의 식을 두 가지 방법으로 표현을 해봤으며 두 표현식에는 간결함의 차이를 보였다. 부울 대수의 조작을 통해서 이러한 표현식의 간결화를 할 수 있다. 진리표와 회로도를 통해 찾는 방법보다 훨씬 간편하고 빠르게 간결화를 할 수 있다. 그러면 F1의 식을 간단하게 만들어보자.

함수의 보수
함수의 보수는 함수의 결과값에 보수를 취한 것이다. 함수 F가 주어졌을 때 F의 보수는 F'이고 그 값은 F = 0이면 F' = 1이고 F = 1이면 F' = 1이 된다. 함수의 보수는 드모르간의 법칙을 통해 증명할 수 있다. 드모르간 법칙은 기본적으로 2개의 변수에 대해 정리되어 있지만 그 이상으로 확장하여 사용할 수 있다. 아래는 3개 변수에 대한 드모르간 법칙 유도이다

위에 유도식을 일반화하면 다음과 같다.

여기서 우리는 함수에 보수를 취할 때는 모든 리터럴에 보수를 취하고 AND와 OR을 서로 바꿔주면 구할 수 있다는 사실을 알 수 있다.
'digital design' 카테고리의 다른 글
| 정준 형식과 표준 형식(Canonical form and Standard form) (0) | 2022.01.21 |
|---|---|
| 부울 대수의 기본 정리와 성질 (0) | 2022.01.19 |
| 부울 대수의 기본 정의와 공리적 정의 (0) | 2022.01.19 |
| Digital Systems and Binary Numbers (0) | 2022.01.16 |