최소항과 최대항(Minterms and Maxterms)
최소항(minterm)또는 표준곱(standard product)이란 하나의 항에 AND로 묶여진 리터럴들을 최소항이라 부른다. 만약 n개의 변수가 있다면 최대 2n개의 최소항을 만들 수 있다. 부울 함수를 최소항으로 표현할 때는 각 항이 1이 되게 하는 조합을 OR로 묶어준다.
최대항(maxterm)또는 표준합(standard sum)은 AND를 기준으로 모든 항들이 OR로 이루어진 형태를 말한다. 최대항 또한 최소항과 같은 2n개의 항을 만들 수 있다. 부울 함수를 최대항으로 나타낼 때는 각 항이 0이 되는 조합을 AND로 묶어준다. 아래 표는 3개의 변수에 대한 최소항과 최대항에 대한 표이다.

표에 있는 각 항들을 보면 서로 보수가 된다는 사실이 보인다. 각 항들은 보수를 취해 서로 변환할 수 있다.
정준 형식(Canonical form)
정준 형식이란 최소항의 합 또는 최대항의 곱 형태로 표현된 부울 함수를 말한다. 이때 각 항은 함수가 가질 수 있는 모든 변수로 표현되어야 된다.
위 표를 이용하여 F = x'yz' + xy'z' + xy(F = 1)을 최소항의 합과 최대항의 곱으로 나타내 보자.
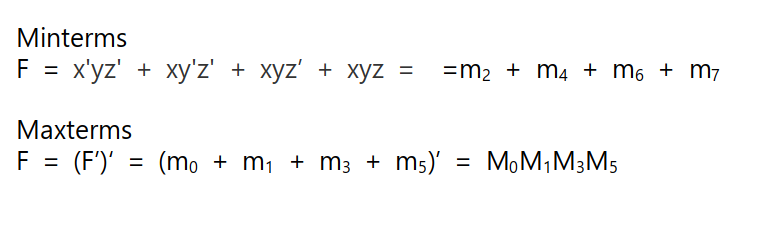
최소항의 합 표현(Sum of Minterms)
함수가 가지는 변수가 n개라면 각 항들을 n개의 변수로 표현해 준다. 함수 F는 3개의 변수를 가지는데 xy는 2개의 변수로만 표현되고 있다. xy는 xyz + xyz'로 표현할 수 있으므로 후자로 변환해준다. 그리고 각 항이 나타내는 적절한 기호로 바꿔준다. 기호로 변환할 때는 각 변수를 '이 있으면 0 없으면 1로 치환하여 나오는 2진수를 사용하면 된다.
x'y'z = m1
최소항의 표현을 간편하게 할 때는 시그마 기호를 이용하여 F = ∑(2, 4, 6, 7)과 같이 표현하기도 한다.
최대항의 곱 표현(Product of Maxterms)
최대항을 표현할 때는 함수의 값이 0이 되는 조합을 찾아야 한다. 최소항을 통해 최대항을 표현할 때는 기존 함수의 보수를 최소항으로 나타내고 함수의 보수에 보수를 취하는 방식으로 최대항 표현을 할 수 있다. 하지만 이는 너무 복잡하다. 최대항의 정의를 이용해 함수가 0이 되는 경우를 곱으로 표현하면 쉽게 표현할 수 있다. 최대항을 표현할 때는 '이 있으면 1 없으면 0으로 표현하여 나오는 2진수를 사용하면 편하게 사용할 수 있다.
(x' + y' + z) = M6
최대항을 표현할 때는 파이 기호를 이용하여 F = ∏(0, 1, 3, 5)로 표현하기도 한다.
정준 형식사이에서의 변환(Conversion between Canonical Forms)
앞에 주어진 함수 F = x'yz' + xy'z' + xy(F = 1)에 대한 진리표를 만들어 보자.

빨간 동그라미가 있는 부분은 F가 1일 때를 가리키고 나머지는 0일 때를 가리킨다. 그러면 우리는 진리표를 통해 F를 최소항의 합이나 최대항의 곱 형태로 나타낼 수 있다. 최소항의 합은 F가 1이 되게 만드는 조합들로 구성되기 때문에 동그라미가 쳐진 항들을 모두 더하면 된다. 최대항의 곱은 동그라미가 쳐지지 않은 항들만 곱으로 표현해주면 된다.
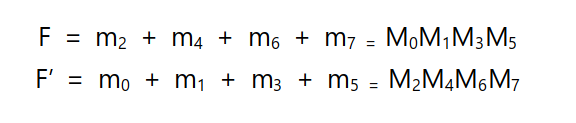
식을 잘 보면 최소항과 최대항으로 나타낼 때 첨자에 있는 숫자가 서로 교차되고 있음을 볼 수 있다. 최소항과 최대항은 서로 보수 관계를 가지며 최소항의 합과 최대항의 곱 사이의 변환은 변수가 만들 수 있는 0~2n-1(n은 변수의 개수)에서 서로 가지고 있지 않는 수를 첨자로 가지는 식을 만들어 주면 된다. 쉽게 말해서 최소항의 합이 2, 4, 6, 7을 가진다면 최대항은 0, 1, 3, 5를 가진다는 것이다.
표준 형식(Standard Forms)
표준형식(standard forms)이란 정준 형식과 다르게 각 항이 가질 수 있는 리터럴의 개수는 임의의 개수를 가진다.
정준 형식에서는 모든 항이 모든 변수로 표현되어지는 반면 표준형식에서는 x + y + z와 같은 형태로 나타낼 수 있다.
표준 형식은 곱의 합과 합의 곱으로 식을 나타낸다.
곱의 합 : F1 = xy + yz
합의 곱 : F2 = (x + y)(y + z)
함수 F1과 F2를 각각 회로도로 나타내면 다음과 같다.
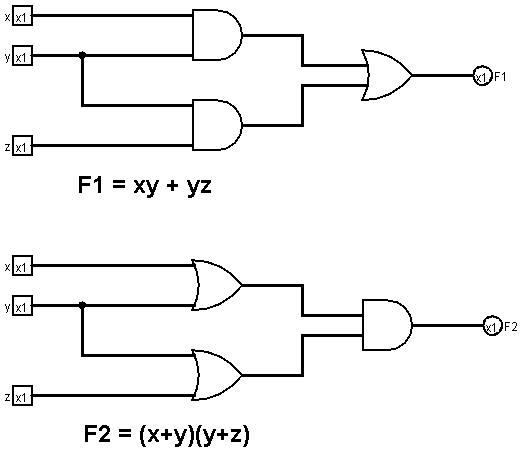
위와 같은 형식을 회로를 2-레벨(two-level)로 구현했다고 한다.
다음 그림은 곱의합도 합의 곱도 아닌 식에 대한 회로도이다.
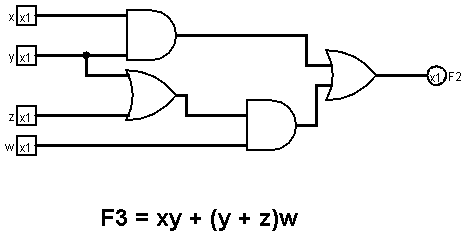
이 회로도는 3-레벨(three-level)로 구성된 회로이다. F3를 표준형식으로 바꾸려면 분배법칙을 통해 괄호를 없애야 한다.
회로도에 레벨을 올리게 되면 각 게이트가 가지는 지연 시간 때문에 속도도 늦어질 뿐 아니라 게이트에 신호가 동시에 전달되게 하기 위해서 여러가지 추가적인 조치가 필요함으로 회로가 복잡해질 수 있다. 그렇기에 회로를 2레벨로 구성하는 것이 가장 효율적이지만 입력이 많아지면 그 또한 문제가 발생하기 때문에 이는 설계자가 상황을 고려하여 적절하게 설계해야 한다.
'digital design' 카테고리의 다른 글
| 부울 함수(Boolean Functions) (0) | 2022.01.20 |
|---|---|
| 부울 대수의 기본 정리와 성질 (0) | 2022.01.19 |
| 부울 대수의 기본 정의와 공리적 정의 (0) | 2022.01.19 |
| Digital Systems and Binary Numbers (0) | 2022.01.16 |