LimeCoding

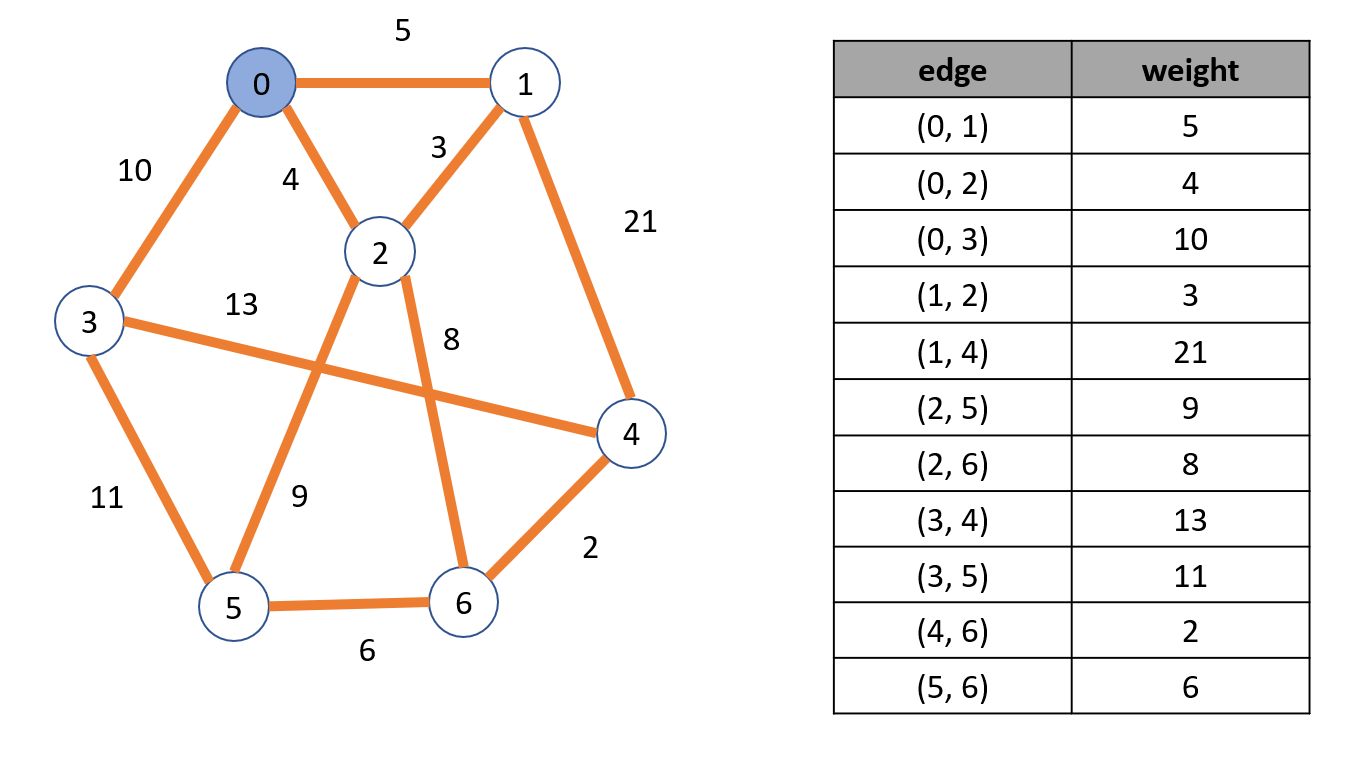
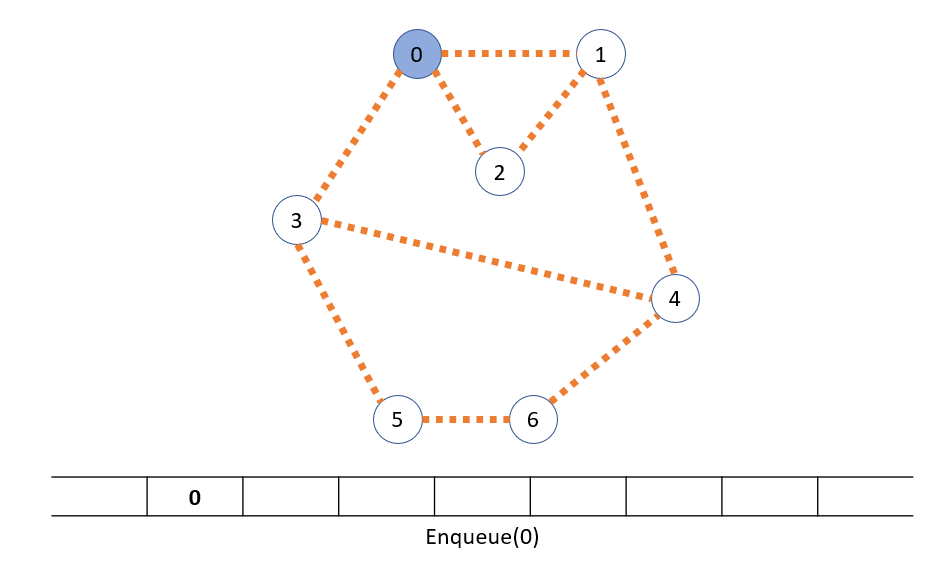
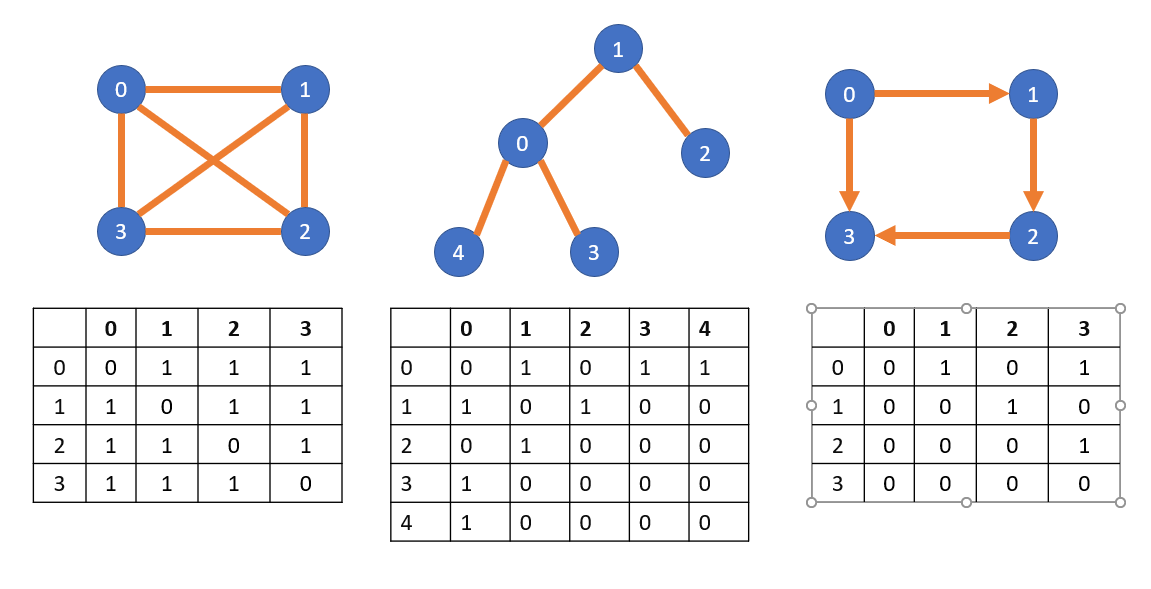
다익스트라 알고리즘이란?(What is a Dijkstra Algorithm?) 다익스트라 알고리즘은 가중치를 가지는 그래프에서 한 정점을 기준으로 다른 정점들에 도달하는 최단 경로를 찾는 알고리즘이다. 이때 중요한 것은 가중치가 음수를 가지면 안된다는 것이다. 가중치가 음수를 가지면 다익스트라 알고리즘이 동작할 수 없다. 다익스트라 알고리즘은 인접한 정점으로 가는 간선중 가장 적은 비용을 가지는 간선을 택한다. 알고리즘 수행중 새로운 경로가 생기면 그 경로를 기록하고 이후에 생기는 또 다른 경로와 비교하면서 최단 경로를 탐색한다. 다익스트라 알고리즘을 수행하기 위해서는 먼저 그래프를 인접 행렬로 표현해야 한다. 위 그림에서 인접 행렬을 보면 무한대 표시가 보인다. 이는 정점이 인접하지 않는다는 표시이다..

솔린 알고리즘이란?(What is a Sollin Algorithm) 솔린 알고리즘은 최소 비용 신장 트리를 구하는 알고리즘중 하나로 크루스칼 알고리즘과 프림 알고리즘처럼 간선을 하나씩 선택하는 것이 아닌 동시에 여러 개의 간선을 선택하여 트리를 만드는 알고리즘이다. 솔린 알고리즘을 설명하기 전 포레스트(Forest)라는 용어의 정의가 필요하다. 포레스트란 서로 연결되지 않은 트리들의 집합 또는 연결되지 않은 비순환 그래프의 집합을 말한다. 그림으로 표시하면 다음과 같다. 그림을 보면 두 그래프는 서로 순환하지 않은 그래프이면서 서로 연결되어 있지 않다. 이런 자료 구조를 포레스트라고 한다.(정점만 있는 그래프나 하나의 트리도 포레스트가 될 수 있다.) 이제 솔린 알고리즘을 설명할 수 있다. 솔린 알고리..

프림 알고리즘이란?(What is a Prime Algorithm) 프림 알고리즘은 최소 비용 신장 트리를 구하는 알고리즘중 하나이다. 가중치를 가지는 그래프에서 가장 작은 가중치를 가지는 엣지를 시작으로 인접한 정점과 연결된 엣지들중 가장 작은 가중치를 가지는 엣지들을 선택해 나가면서 신장 트리를 만드는 것이 프림 알고리즘이다. 프림 알고리즘이 엣지를 하나씩 선택한다는 점에서는 크루스칼 알고리즘과 같지만 인접한 정점의 엣지들만 선택한다는 점에서는 크루스칼 알고리즘과 다른 점을 보여준다. 다음은 프림 알고리즘 수행 과정이다. 그래프 및 가중치 표 다음은 프림 알고리즘에 사용될 그래프와 그래프의 가중치를 표로 나타낸 것이다. 그럼 프림 알고리즘을 수행해보자. (4, 6) 선택 먼저 시작은 가장 작은 가중치..

크루스칼 알고리즘이란?(What is a Kruskal Algorithm?) 최소 비용 신장 트리를 구하는 알고리즘중 하나인 크루스칼 알고리즘은 가중치가 부여된 그래프 G = (V, E)가 있을 때 그래프 G를 이루는 G(V)에 대해 가장 가중치가 낮은 엣지부터 각 정점들이 모두 연결될 때까지 간선을 추가한다. 이때 엣지는 사이클이 만들어지지 않는 엣지만 선택해야한다. 그래프가 n개의 정점으로 이루어져 있다면 가중치가 가장 낮은 엣지부터 시작해서 n-1개의 엣지를 선택하여 만들면 된다. 만약 n-1개 미만의 엣지만이 존재한다면 이는 그래프가 애초에 연결 그래프가 아닌 상태이다. 다음은 크루스칼 알고리즘을 이용한 최소 비용 신장 트리 구성 방법이다. 그래프의 초기 상태 및 각 엣지의 가중치 그래프의 형태와..

오늘 글을 5개나 썼다. 내일 책을 반납해야하는데 목표한 챕터까지 글을 아직 못써서 지금 열심히 쓰는 중이다. 지금까지는 내가 시간이 오래걸리는 거라 생각했는데 그게 맞다. 근데 원인이 내가 아니라 집중을 안하는 것이였다. 이번에 집중에서 이해하고 자료 찾아가면서 쓰니까 거의 1시간에 1개씩 쓰고 있다. 물론 1챕터에 대해서만 쓰고 있는거긴 한데 그래도 글이 많이 써지긴 한다. 지금까지는 공부할 시간이 없는게 아니라 너무 많이 쳐 노니까 그만큼 시간이 뺏긴거다. 최근에 친구가 백준 문제를 엄청나게 빠른 속도로 풀고 있다. 평소에 공부를 안하는 친구인데 그런 속도로 쫓아오니까 나도 살짝 겁이 난다. 뭔가 엄청나게 공부하고 공부한 내용을 글로 쓰는 생산이 필요한 것 같다. 그래서 공부하는 기계처럼 계속 공부..

신장 트리란?(What is a Spanning Tree?) 앞서 포스팅에서 깊이 우선 탐색과 너비 우선 탐색에 대해 다루었다. 연결 그래프 G = (V, E)에 대해서 깊이 우선 탐색이나 너비 우선 탐색을 하게 되면 정점들을 방문하면서 지나는 엣지들을 보면 트리 형태의 모양을 띄게 된다. 이러한 그래프를 탐색하면서 지나게 되는 엣지들의 집합을 트리 엣지(tree edge)라고 하고 트리 엣지를 제외한 나머지 엣지들을 비트리 엣지(nontree edge)라고 한다. 깊이 우선 탐색이나 너비 우선 탐색을 하게 되면 생기는 트리엣지로 이루어진 사이클을 갖지 않는 최소 부분 그래프가 생기는데 이 부분 그래프를 그래프 G에 대한 신장 트리라고 한다. 만약 n개의 정점을 가지는 그래프가 있다면 n개의 정점을 모두..

너비 우선 탐색(Breadth First Search)는 BFS라고도 하며 그래프를 순회하는 방법중 하나이다. 너비 우선 탐색은 깊이 우선 탐색과 다르게 인접한 정점을 모두 방문한 후 정점을 방문한 순서대로 다시 모든 인접한 정점을 방문하는 방식의 탐색 방법이다. 너비 우선 탐색은 큐로 구현을 할 수 있다. 너비 우선 탐색 방법은 다음과 같다. 너비 우선 탐색이 시작될 정점 v를 선택한다. 선택된 정점 v에 대해 방문 표시와 방문 처리를 하고 큐에 삽입한다. 큐의 front에서 꺼낸 정점의 인접 정점들에 대해 방문되지 않은 정점들을 큐에 삽입하고 방문 처리를 한다. 큐가 공백이 될 때까지 3의 과정을 반복한다. 다음은 너비 우선 탐색의 예시이다. 정점 0 방문 정점 0을 방문한 후 큐에 0을 넣는다. 정..

깊이 우선 탐색(Depth First Search)은 DFS라고도 불리며 그래프를 순회하는 방법 중에 하나이다. 깊이 우선 탐색은 한 정점을 기준으로 인접한 정점을 방문한 뒤 방문한 정점을 기준으로 다시 인접한 정점을 방문하는 방식의 재귀적인 방법으로 방문을 한다. 깊이 우선 탐색은 다음과 같은 방법으로 진행된다. 깊이 우선 탐색을 시작할 정점을 선택한다. 선택된 정점을 방문 처리한다. 정점 v에 인접한 정점들에 대해 3-1. 방문되지 않은 정점이 존재하면 정점 v를 스택에 push하고, v의 인접 정점들 가운데 방문되지 않은 정점 w를 선택하여 2의 과정부터 다시 시작한다. 3-2. 방문되지 않은 정점이 존재하지 않는다면 가장 최근에 스택에 push된 정점을 pop하여 3의 과정부터 다시 사작한다. s..

인접 행렬(Adjacency Matrix) 컴퓨터로 그래프를 표현하는 방법중 하나는 인접 행렬이다. 인접 행렬은 배열을 이용하여 표현한다. 여기서 배열의 행은 출발 노드를 가리키고 열은 도착 노드를 가리킨다. 두 노드의 경로가 존재하면 1, 존재하지 않으면 0으로 표기한다. 무방향 그래프는 1->0과 0->1로 가는 경로를 모두 표기하고 방향 그래프는 해당 경로가 있는 경우에만 표시를 한다. 위 표를 자세히 보면 알 수 있는 재미있는 사실이 하나 있다. 그건 바로 첫 번째 그래프와 두 번째 그래프의 인접 행렬은 모두 대각선에 대해 대칭 형태를 보여준다. 그렇기 때문에 대각선으로 나누어지는 배열의 반만 있어도 그래프를 표현할 수 있다. 세 번째 그래프의 경우도 1보다는 0이 더 많은 것을 볼 수 있다. 이..

그래프란?(What is a Graph?) 그래프의 개념은 1736년 수학자 레온하르트 오일러가 쾨니히스베르크의 다리에 대한 문제를 풀면서 처음 등장했다. 오일러는 각 섬을 정점으로 표현하고 다리는 엣지로 표현하면서 모든 다리를 한번씩만 거쳐서 원래대로 돌아오는 방법은 존재하지 않는다는 것을 증명했다. 이러한 그래프는 현대에 와서는 전기 회로의 분석, 최단 경로 검색, 컴퓨터 통신 네트워크, 인공지능등 많은 분야에서 사용되고 있다. 자료구조에서 그래프(graph)는 공집합이 아닌 정점들(vertex)의 집합과 이 정점들을 서로 연결하는 엣지들의 집합으로 정의할 수 있다. 그래프에서 정점(vertex)은 데이터를 가지는 노드이며, 서로 다른 두 정점을 잇는 선을 엣지(edge) 또는 간선이라고 한다. 그래..